
Warner Bruns
December 1, 2002

We got detailed technical drawings1 of a Doris cavity.
The data from these drawings are transformed step by step into an inputfile for gd1. Every step is explained in detail. Numerous hints are given, how one effectively models ones geometry. When we have modelled the geometry accurately enough, we compute the fields and wakepotentials.
 |
In the first step we model the cavity and the beam-pipes. We do this by specifying a polygonal description of the boundary in the r-z-plane. The inputfile that describes the boundary is:
#
# Some helpful symbols:
#
define(EL, 1) define(MAG, 2)
define(INF, 1000)
#
# We define symbols that will be used to describe our cavity:
# The names of the symbols can be up to 32 characters long,
#
define(OuterRadius , 46.23e-2/2 )
define(InnerRadius , 13.00e-2/2 )
define(GapLength , 27.60e-2 )
define(CurveRadius , 0.585e-2 )
define(BeamPipeRadius, 14.17e-2/2 )
define(TaperLength , 13.2e-2 )
-brick
material= EL
xlow= -INF, xhigh= INF
ylow= -INF, yhigh= INF
zlow= -INF, zhigh= INF
doit
#
# we carve out the body of the cavity
#
-gbor
material= 0
origin= (0,0,0)
zprimedirection= (0,0,1)
rprimedirection= (1,0,0)
range= (0,360)
clear # clear any old polygon-description
# point= (z,r)
point= ( -(GapLength/2+TaperLength+10e-2), 0 ) # p1
point= ( -(GapLength/2+TaperLength+10e-2), BeamPipeRadius )
point= ( -(GapLength/2+TaperLength ), BeamPipeRadius )
point= ( -(GapLength/2+CurveRadius ), InnerRadius )
arc, radius= CurveRadius, size= small, type= counterclockwise
point= ( -(GapLength/2 ), InnerRadius+CurveRadius )
point= ( -(GapLength/2 ), OuterRadius )
## crossing z=0 plane
point= ( (GapLength/2 ), OuterRadius )
point= ( (GapLength/2 ), InnerRadius+CurveRadius )
arc, radius= CurveRadius, size= small, type= counterclockwise
point= ( (GapLength/2+CurveRadius ), InnerRadius )
point= ( (GapLength/2+TaperLength ), BeamPipeRadius )
point= ( (GapLength/2+TaperLength+10e-2), BeamPipeRadius )
point= ( (GapLength/2+TaperLength+10e-2), 0 )
show= now
doit
-volumeplot
doit
This inputfile can be found as "/usr/local/gd1/Tutorial-SRRC/doris00.gdf".
When we feed this file into gd1 via the command
"gd1 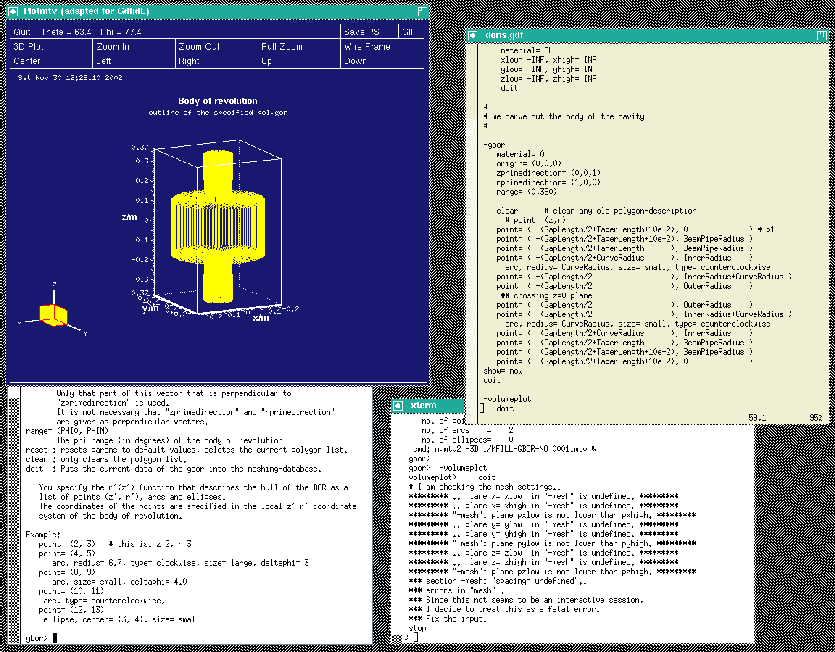 |
gd1 does not what we want, we do not get a "volumeplot", although we requested one. But gd1 gives us a hint what we made wrong:
volumeplot> doit # I am checking the mesh settings.. .. plane x= xlow in "-mesh" is undefined.. .. plane x= xhigh in "-mesh" is undefined.. .. plane y= ylow in "-mesh" is undefined.. .. plane y= yhigh in "-mesh" is undefined.. .. plane z= zlow in "-mesh" is undefined.. .. plane z= zhigh in "-mesh" is undefined.. *** section -mesh: "spacing= undefined".. *** errors in "mesh".. *** Since this not seems to be an interactive session, *** I decide to treat this as a fatal error. *** Fix the input. stopWhen we say "doit" in the section "-volumeplot", gd1 tries to generate the mesh. But in order to generate the mesh, gd1 needs to know
To give gd1 the needed information, we change our inputfile. We insert the following lines somewhere before "-volumeplot":
###
### We define the borders of the computational volume,
### and we define the default mesh-spacing.
###
-mesh
spacing= InnerRadius/15
pxlow= -1.1*OuterRadius, pxhigh= 1.1*OuterRadius
pylow= -1.1*OuterRadius, pyhigh= 1.1*OuterRadius
pzlow = -(GapLength/2+TaperLength+9e-2)
pzhigh= +(GapLength/2+TaperLength+9e-2)
The so edited inputfile can be found as
"/usr/local/gd1/Tutorial-SRRC/doris01.gdf".
When we feed gd1 with this inputfile (gd1 ![]() doris01.gdf)
we get a screen similiar to the one shown in figure 1.4
doris01.gdf)
we get a screen similiar to the one shown in figure 1.4
 |
-mesh.
We edit our inputfile so that it contains
-mesh
#
# enforce two meshplanes, at the bottom and the top of the cavity:
#
zfixed(2, -GapLength/2, GapLength/2 )
The semantics of zfixed(N, Z0, Z1) is:
N is the number of meshplanes to enforce,
the meshplanes are placed equidistantly between Z0 and Z1.
It is allowed to specify positions of mesh-planes that are outside of the
computational volume.
Since we have had already a quite fine mesh, the effect is not visible and is not shown here.
There is not much gain if one tries to enforce meshplanes at the outer radii of the cavity and the beam-pipes.
We specify that we only want to compute in the volume
![]() by specifying the borders of the computational
volume accordingly.
We change the specifications in the inputfile to
by specifying the borders of the computational
volume accordingly.
We change the specifications in the inputfile to
###
### We define the borders of the computational volume,
### and we define the default mesh-spacing.
###
-mesh
spacing= InnerRadius/15
pxlow= -1.1*OuterRadius
pylow= -1.1*OuterRadius
pzlow = -(GapLength/2+TaperLength+9e-2)
pxhigh= 0
pyhigh= 0
pzhigh= 0
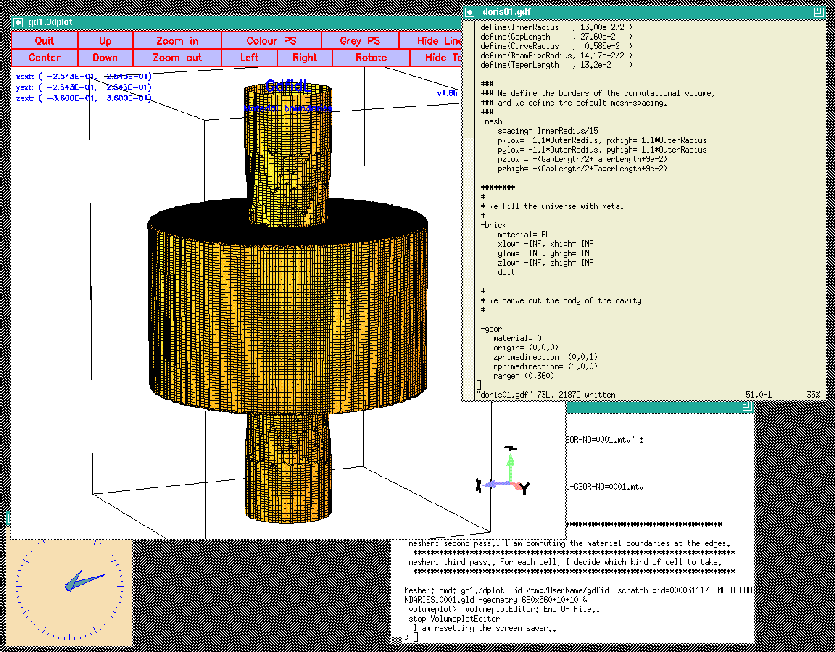
When we feed gd1 with this inputfile (gd1 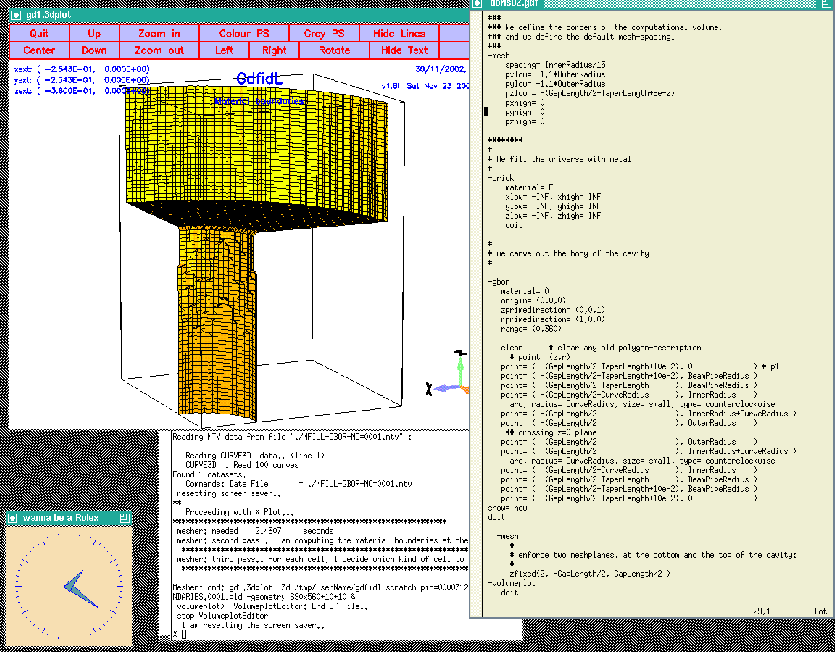 |
-mesh". We edit our
inputfile such that the entries for -mesh now look like:
###
### We define the borders of the computational volume,
### we define the default mesh-spacing,
### and we define the conditions at the borders:
###
-mesh
spacing= InnerRadius/15
pxlow= -1.1*OuterRadius
pylow= -1.1*OuterRadius
pzlow = -(GapLength/2+TaperLength+9e-2)
pxhigh= 0
pyhigh= 0
pzhigh= 0
#
# The conditions to use at the borders of the computational volume:
#
cxlow= electric, cxhigh= magnetic
cylow= electric, cyhigh= magnetic
czlow= electric, czhigh= electric
We are not done yet: Since gd1 can compute resonant fields and time
dependent fields, we have to specify what kind of field we are interested in.
We want to compute resonant fields, so we specify this by entering at the
end of our inputfile:
-eigenvalues
solutions= 15 # we want to compute with 15 basis vectors
estimation= 10e9 # the estimated highest frequency
doit
When we feed gd1 with this inputfile (gd1 *** A component of the path prefix does not exist or the Path parameter points *** to an empty string. CreateDirectory: cmd: mkdir /tmp/--username--/--SomeDirectory--/Results error code: 2 ** cannot open catalogue: iostat: 14 ** catalogue: "/tmp/--username--/--SomeDirectory--/Results/catalogue" ** error msg: "No such file or directory / permission denied" InitializeDatabase: cannot read catalogue.. iostat: 14 *** check "outfile" in section "-general".. *** errors in settings *** Since this not seems to be an interactive session, *** I decide to treat this as a fatal error. *** Fix the input. stopWe have not yet specified where the results of your computation shall be written to! We do this by editing our inputfile:
###
### We enter the section "-general"
### Here we define the name of the database where the
### results of the computation shall be written to.
### (outfile= )
### We also define what names shall be used for scratchfiles.
### (scratchbase= )
###
-general
outfile= /tmp/UserName/doris
scratchbase= /tmp/UserName/doris-scratch
#
# Some helpful symbols:
#
define(EL, 1) define(MAG, 2)
define(INF, 1000)
#
# We define symbols that will be used to describe our cavity:
# The names of the symbols can be up to 32 characters long,
#
define(OuterRadius , 46.23e-2/2 )
define(InnerRadius , 13.00e-2/2 )
define(GapLength , 27.60e-2 )
define(CurveRadius , 0.585e-2 )
define(BeamPipeRadius, 14.17e-2/2 )
define(TaperLength , 13.2e-2 )
###
### We enter the section "-general"
### Here we define the name of the database where the
### results of the computation shall be written to.
### (outfile= )
### We also define what names shall be used for scratchfiles.
### (scratchbase= )
###
-general
outfile= /tmp/UserName/doris
scratchbase= /tmp/UserName/doris-scratch
###
### We define the borders of the computational volume,
### and we define the default mesh-spacing.
###
-mesh
spacing= InnerRadius/15
pxlow= -1.1*OuterRadius
pylow= -1.1*OuterRadius
pzlow = -(GapLength/2+TaperLength+9e-2)
pxhigh= 0
pyhigh= 0
pzhigh= 0
#
# The conditions to use at the borders of the computational volume:
#
cxlow= electric, cxhigh= magnetic
cylow= electric, cyhigh= magnetic
czlow= electric, czhigh= electric
########
#
# We fill the universe with metal
#
-brick
material= EL
xlow= -INF, xhigh= INF
ylow= -INF, yhigh= INF
zlow= -INF, zhigh= INF
doit
#
# we carve out the body of the cavity
#
-gbor
material= 0
origin= (0,0,0)
zprimedirection= (0,0,1)
rprimedirection= (1,0,0)
range= (0,360)
clear # clear any old polygon-description
# point= (z,r)
point= ( -(GapLength/2+TaperLength+10e-2), 0 ) # p1
point= ( -(GapLength/2+TaperLength+10e-2), BeamPipeRadius )
point= ( -(GapLength/2+TaperLength ), BeamPipeRadius )
point= ( -(GapLength/2+CurveRadius ), InnerRadius )
arc, radius= CurveRadius, size= small, type= counterclockwise
point= ( -(GapLength/2 ), InnerRadius+CurveRadius )
point= ( -(GapLength/2 ), OuterRadius )
## crossing z=0 plane
point= ( (GapLength/2 ), OuterRadius )
point= ( (GapLength/2 ), InnerRadius+CurveRadius )
arc, radius= CurveRadius, size= small, type= counterclockwise
point= ( (GapLength/2+CurveRadius ), InnerRadius )
point= ( (GapLength/2+TaperLength ), BeamPipeRadius )
point= ( (GapLength/2+TaperLength+10e-2), BeamPipeRadius )
point= ( (GapLength/2+TaperLength+10e-2), 0 )
show= now
doit
-mesh
#
# enforce two meshplanes, at the bottom and the top of the cavity:
#
zfixed(2, -GapLength/2, GapLength/2 )
-volumeplot
## doit
-eigenvalues
solutions= 15
estimation= 10e9 # the estimated highest frequency
doit
boundary conditions:
xboundary= electric, magnetic
yboundary= electric, magnetic
zboundary= electric, electric
--------------------
i freq(i) acc(i) cont(i)
1 503.4599e+6 0.0037654709 0.0027611672 # "grep" for me
2 1.1576e+9 0.0363792177 0.0338547693 # "grep" for me
3 1.2000e+9 0.0270761163 0.0465387932 # "grep" for me
4 1.5669e+9 0.1173770231 0.2662151486 # "grep" for me
5 1.7357e+9 0.4963611925 1.0000000000 # "grep" for me
6 1.9216e+9 0.1752955583 0.5479572604 # "grep" for me
7 2.2211e+9 0.0811233028 0.3181446327 # "grep" for me
8 2.4446e+9 0.1903593461 0.8610742652 # "grep" for me
9 2.7054e+9 0.1513682675 0.5798372263 # "grep" for me
10 3.0470e+9 0.2475596875 1.0000000000 # "grep" for me
11 3.2898e+9 0.0970269338 0.4556358188 # "grep" for me
12 3.6312e+9 0.1308660265 0.5174922697 # "grep" for me
13 4.0755e+9 0.1248055514 0.5934680518 # "grep" for me
14 4.3644e+9 0.0810408709 0.2603226655 # "grep" for me
15 5.0381e+9 0.0901497971 0.3161751272 # "grep" for me
################################
# cpu-seconds for eigenvalues : 47
# start date : 30/11/2002
# end date : 30/11/2002
# start time : 13:00:26
# end time : 13:01:32
# The computation of the eigenvalues has finished normally..
# Start the postprocessor to look at the results.
stop .. normal end ..
We see that the results are very bad. The accuracy of all modes is horrible.
The reason for this is: We did specify a badly wrong estimation of the highest
resonant frequency (We did specify estimation= 10e9).
We change the inputfile such that we have
-eigenvalues
solutions= 15
estimation= 2e9 # the estimated highest frequency
doit
When we compute with the adjusted estimation
(gd1
boundary conditions:
xboundary= electric, magnetic
yboundary= electric, magnetic
zboundary= electric, electric
--------------------
The first 2 solutions seem to be static and are not saved.
i freq(i) acc(i) cont(i)
1 503.4601e+6 0.0000000341 0.0000000180 # "grep" for me
2 1.0594e+9 0.0000000000 0.0000000000 # "grep" for me
3 1.1579e+9 0.0000000010 0.0000000060 # "grep" for me
4 1.2001e+9 0.0000000003 0.0000000038 # "grep" for me
5 1.2528e+9 0.0000000000 0.0000000000 # "grep" for me
6 1.5070e+9 0.0000000001 0.0000000002 # "grep" for me
7 1.5445e+9 0.0000000001 0.0000000017 # "grep" for me
8 1.5679e+9 0.0000000028 0.0000000893 # "grep" for me
9 1.5926e+9 0.0000000003 0.0000000026 # "grep" for me
10 1.6717e+9 0.0000000002 0.0000000021 # "grep" for me
11 1.7208e+9 0.0000000139 0.0000002458 # "grep" for me
12 1.7544e+9 0.0000004046 0.0000086559 # "grep" for me
13 1.7950e+9 0.0000025979 0.0000567143 # "grep" for me
################################
# cpu-seconds for eigenvalues : 102
# start date : 30/11/2002
# end date : 30/11/2002
# start time : 13:04:35
# end time : 13:06:40
# The computation of the eigenvalues has finished normally..
# Start the postprocessor to look at the results.
stop .. normal end ..
These results are accurate enough for now.
-general. We can specify the name
of the resultfile in two ways: By writing out the name of the file:
-general, infile= /tmp/UserName/dorisor by using the special name
@last:
-general, infile= @lastWhen we use
@last,
gd1.pp looks up the name of the last resultfile in
a special file $HOME/name.of.last.gdfidl.file. This file is written
by every run of gd1.
By the way: Both gd1 and gd1.pp understand almost all their commands also when they are abbreviated. So we may tell gd1.pp to take the last resultfile eg. as follows:
-ge, i @last
-3darrowplot,
and tell gd1.pp that we want to look at the electric field pattern of the first
stored field:
-3darrowplot
symbol= e_1
doit
Abbreviated we may say eg. -3da, sy e_1, dWe can look at several plots simultaneously. We just say that we want to have another plot, and gd1.pp starts another instance of gd1.3dplot to show the plot. To have a look at the first three modes, we say eg.
quantity= e solution= 1, doit so 2, doit so 3, doitThe figure 3.1 shows the resulting desktop.
 |
quantity= h,
or we specify as symbol eg. symbol= h_1:
-3darrow
quantity= h
solution= 1, doit
solution= 2, doit
solution= 3, doit
The figure 3.2 shows the resulting desktop.
 |
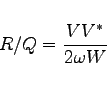 |
(3.1) |
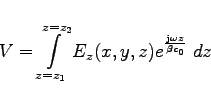 |
(3.2) |
We now enter the relevant sections of gd1.pp and explain how the quantities that show up in the above formula can be computed.
-lintegral.
Its menu is:
############################################################################## # Flags: nomenu, prompt, message, # ############################################################################## # section: -lintegral # ############################################################################## # symbol = e_1 # # quantity = e # # solution = 1 # # # # direction = z # # component = z # # startpoint= ( 0.0, 0.0, -1.0e+30 ) # # (used) : ( @x0: undefined, @y0: undefined, @z0: undefined ) # # length = auto # # (@length) : undefined # # beta = 1.0 # # frequency = auto -- [auto | Real] # ############################################################################## # @vreal= undefined @vimag= undefined @vabs= undefined # ############################################################################## # doit, ?, return, end, help # ##############################################################################In order to compute our voltage, we have to specify what field shall be integrated, what component of the field shall be integrated, along which direction we want to perform the integration, and what the startpoint shall be. We specify this and perform the integration (
doit):
-lintegral
symbol= e_1
direction= z
component= z
startpoint= ( 0, 0, @zmin)
length= auto
doit
Upon entering "?",
gd1.pp shows us the changed menu now as:
############################################################################## # Flags: nomenu, prompt, message, # ############################################################################## # section: -lintegral # ############################################################################## # symbol = e_1 # # quantity = e # # solution = 1 # # # # direction = z # # component = z # # startpoint= ( 0.0, 0.0, -360.0e-3 ) # # (used) : ( @x0: 0.0, @y0: 0.0, @z0: -360.0e-3 ) # # length = auto # # (@length) : 360.0e-3 # # beta = 1.0 # # frequency = auto -- [auto | Real] # ############################################################################## # @vreal= 13.88403 @vimag= -14.67090 @vabs= 20.19905 # ############################################################################## # doit, ?, return, end, help # ##############################################################################We see the startpoint that we entered is the same as the startpoint actually taken, the length of the integration path is 360 mm, and the result of the integration is: Real part is 13.88403
Volts,
imaginary part is -14.67090 Volts,
and the absolute value of the voltage is 20.19905 Volts.
We can write these numbers down on paper, but we can also compute with them
within gd1.pp. They are accessible as symbolic variables
@length, @vreal, @vimag, @vabs.
We will use these variables later.
For our shunt impedance computation, we have to decide what value of the
three values we have to take.
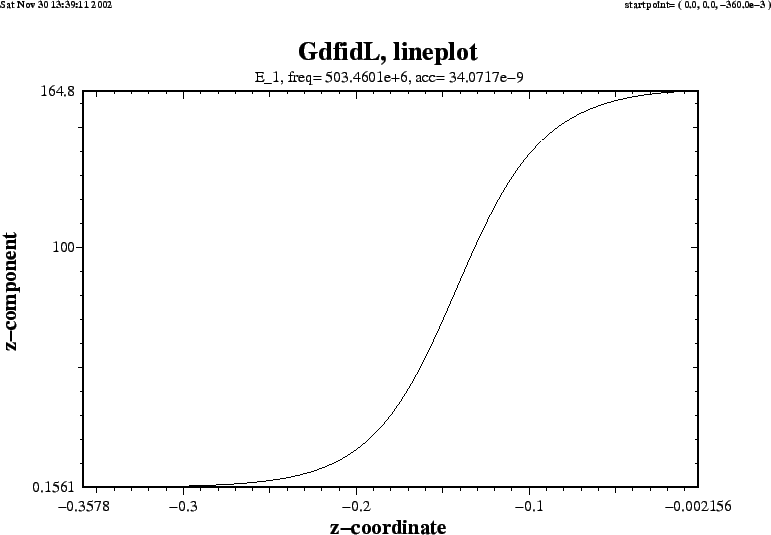
From a plot of the accelerating field strength as it is shown in figure
3.3, we see that the field strength is even with respect to the plane
z=0. The accelerating voltage that would be seen by a particle traversing the
whole structure would therefore be twice the real part of the voltage in the
half structure. In a full structure, the imaginary part of the complex voltage
would vanish. We therefore have to take as ![]() four times the square of
the real part
four times the square of
the real part @vreal.
 |
-energy is:
############################################################################## # Flags: nomenu, prompt, message, # ############################################################################## # section: -energy # ############################################################################## # symbol = e_1 # # quantity = e # # solution = 1 # # # # # # @henergy : undefined (symbol: undefined, m: 1) # # @eenergy : undefined (symbol: undefined, m: 1) # ############################################################################## # doit, ?, return, end, help # ##############################################################################We have to know both the energy in the electric field and in the magnetic field. But since the fields are resonant fields, the energies are the same for both types of fields. So it suffices to compute only the energy in the electric field:
-energy
quantity= e
solution= 1
doit
The result of the energy computation is now available in the menu, as well
as the value of the symbolic variable @eenergy.
############################################################################## # Flags: nomenu, prompt, message, # ############################################################################## # section: -energy # ############################################################################## # symbol = e_1 # # quantity = e # # solution = 1 # # # # # # @henergy : undefined (symbol: undefined, m: 1) # # @eenergy : 98.21061e-12 (symbol: e_1, m: 2) # ############################################################################## # doit, ?, return, end, help # ##############################################################################Since we have modelled only the eighth part of the structure (we did use all three symmetry planes), the stored energy in the electric field of the whole structure is 8 times as high as
@eenergy=98.21061e-12 Ws.
We now have all the necessary numbers to compute the normalized shunt impedance of this first mode:
@vreal = 13.88,
@frequency,
@eenergy.
echo shuntimpedance is \ eval((2*@vreal)*(2*@vreal) / (2*@pi*@frequency * 8*2*@eenergy) ) Ohms
The full input for the postprocessor:
-general
infile= @last
-energy
symbol= e_1
doit
-lintegral
component= z, direction= z
startpoint= (0,0,@zmin)
doit
echo frequency is: eval(@frequency/1e6) MHz
echo shuntimpedance is \
eval((2*@vreal)*(2*@vreal) / (2*@pi*@frequency * 8*2*@eenergy) ) Ohms
gd1.pp tells us then:
frequency is: 503.4601030 MHz shuntimpedance is 155.11998650323 Volts
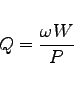 |
(3.3) |
-wlosses.
Its menu is:
############################################################################## # Flags: nomenu, prompt, message, # ############################################################################## # section: -wlosses # ############################################################################## # symbol = e_1 # # quantity = e # # solution = 1 # # frequency = auto -- [auto | Real] # # # # # # @metalpower : undefined (symbol: undefined) # ############################################################################## # doit, ?, return, end, help # ##############################################################################Since the power losses are caused by currents flowing in metal, and the currents are proportional to the tangential H-field at the metallic walls, we have to enter a H-field as
symbol or quantity.
-wlosses
quantity= h
solution= 1
doit
The wall losses are computed as:
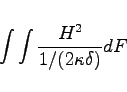 |
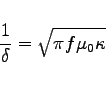 |
The integral is performed over all metallic surfaces that would appear in a plot as produced by the section -3darrowplot. This implies, that wall losses are NOT computed for electric symmetry planes, since the material on the symmetry planes are not shown in -3darrowplot.
The conductivities that are used in the pertubation formula may be entered in the section -material. The result of the computation is available as the symbolic variable @metalpower.
The resulting menu (with the default conductivities of copper) is
############################################################################## # Flags: nomenu, prompt, message, # ############################################################################## # section: -wlosses # ############################################################################## # symbol = h_1 # # quantity = h # # solution = 1 # # frequency = auto -- [auto | Real] # # # # # # @metalpower : 16.21816e-6 (symbol: h_1) # ############################################################################## # doit, ?, return, end, help # ##############################################################################
It suffices to compute the voltage at different paths, the stored energy
of course is independent of the position (x,y).
We compute the voltages at all positions (xi,0) and (0,yi) that are available
in the grid. These positions of the grid planes are available in gd1.pp
as the symbolic functions @x(i), @y(i), @z(i).
The total number of grid planes are available as @nx, @ny, @nz.
These symbols are only available after a database has been specified in
-general.
So, to compute the voltages at all possible positions (xi,0) we may say:
-lintegral
symbol= e_1
direction= z, component= z
do ix= 1, @nx
startpoint= ( @x(ix), 0, @zmin )
doit
echo voltage along ( @x0 , @y0 , z=z ) is @vreal @vimag @vabs
enddo
If we do this, we get a lot of messages on the screen.
In order to have a nice graphic of the dependence of the voltage on x,
we better redirect the output to a file and process the result slightly.
We write a small shell script:
#!/bin/sh
#
# feed the postprocessor with a 'here'-document,
# 'tee' the output of the postprocessor to the file "pp.out"
#
(gd1.pp | tee pp.out) << EOF
nomenu, noprompt, nomessage # no unneccessary output
-general, infile= @last
-lintegral
symbol= e_1
direction= z, component= z
do ix= 1, @nx
startpoint= ( @x(ix), 0, @zmin )
doit
echo @x0 @vreal @vimag # <= x, vreal, vimag
enddo
end
EOF
#
# Write a PlotMtv-header to "x-voltages.mtv".
#
# Process the file "pp.out":
# 'grep' the lines with the pattern "vreal"
#
echo \$ DATA= COLUMN > x-voltages.mtv
echo x vreal vimag >> x-voltages.mtv
grep vreal pp.out >> x-voltages.mtv
#
# now start "mymtv2" to display the data:
#
mymtv2 -mult -landscape x-voltages.mtv
3.4
This shell-script can be found as "/usr/local/gd1/Tutorial-SRRC/x-voltages.x".
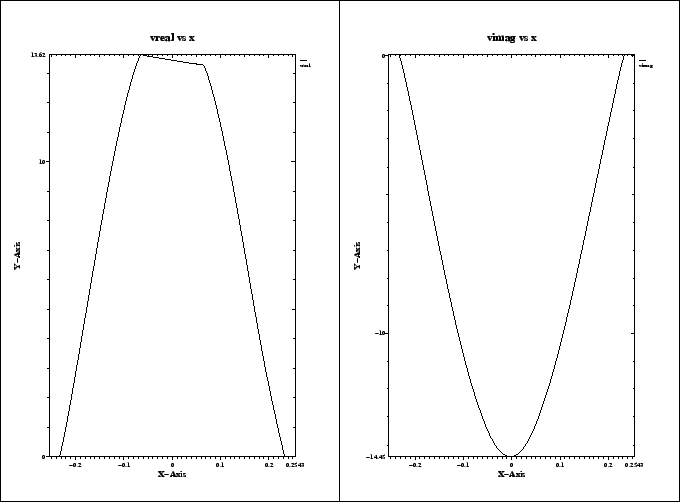
The resulting plot is shown in figure 3.4.
We see that the real part of the integrated voltage is almost constant in the
range
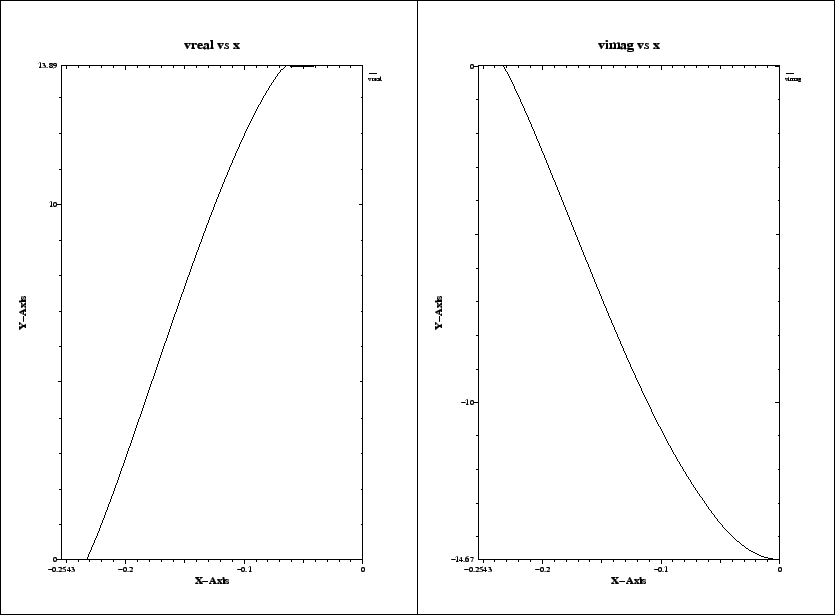 |
-mesh
define(STPSZE, InnerRadius/15)
spacing= STPSZE
pxlow= -1.1*OuterRadius
pylow= -1.1*OuterRadius
pzlow = -(GapLength/2+TaperLength+9e-2)
pxhigh= 0
pyhigh= 0
pzhigh= (GapLength/2+TaperLength+9e-2)
For the linecharge, we have to specify its total charge, its length,
and the (x,y)-position where it shall travel.
We also have to say that we do not want to compute eigenvalues, but we want to
perform a time domain computation.
We specify that at the lower and upper z-planes absorbing boundary
conditions shall be applied.
In the section -time, we specify that we want to have saved
the fields at 90 equidistant times between the time that the line charge
has traveled 0.1 m and it has traveled 1 m.
We edit our inputfile, such that the end of it looks as:
-eigenvalues
solutions= 15
estimation= 2e9 # the estimated highest frequency
# doit
-fdtd
-lcharge
charge= 1e-12
sigma= 4*STPSZE
xposition= 0, yposition= 0
shigh= 1.5
showdata= yes
-ports
name= beamlow , plane= zlow, modes= 3, npml= 40, doit
name= beamhigh, plane= zhigh, modes= 3, npml= 40, doit
-time
firstsaved= 0.1/@clight
lastsaved= 1/@clight
distancesaved= 0.1/@clight
-fdtd
doit
The so edited inputfile can be found as
"/usr/local/gd1/Tutorial-SRRC/doris05-wake.gdf".
We start the computation by feeding gd1 the inputfile:
gd1 < doris05-wake.gdf | tee outThe computation only takes some minutes, since we compute a short range wake. When the time domain iteration starts, gd1 detects that the specified wake path is tangential to two magnetic walls. gd1 spits out:
## I am iterating Yee's algorithm.. ################### # wake-computation: # (x,y)-position of the line charge: # specified (x,y)-position : ( 0.00000000 , 0.00000000 ) # used (x,y)-position : ( 0.00000000 , 0.00000000 ) # ix, iy : 60, 60 # min. distances : 0.00000000 .. 0.00000000 ############ I am checking the beam-path.. #-- charge travels at upper x-plane. #-- charge travels at upper y-plane. ######################### # Wake computation: # Since the charge travels along one or two symmetry-planes, # only 25 % of the charge is considered traveling through # the computational volume. # The excited fields in the subvolume will be the same as if # you were computing without the symmetry planes. # The lossfactors as computed by the post-processor will be # the same also. #########################The end of the output of gd1 (on a reasonably fast machine) is:
timestep= 800, simulated time= 6.2198e-9 s wakepotentials are known up to s= 1.1353 m cpu time/sec: used: 64.11, since last call: 7.41, MFLOPs/s: 88.69 Wall clock time: 71.00 s, MFLOPs/s: 80.08 timestep= 900, simulated time= 6.9973e-9 s wakepotentials are known up to s= 1.3672 m cpu time/sec: used: 71.52, since last call: 7.41, MFLOPs/s: 89.45 Wall clock time: 79.00 s, MFLOPs/s: 80.98 The highest simulation time is reached .., I am stopping ################################ # cpu-seconds for FDTD : 75 # start date : 30/11/2002 # end date : 30/11/2002 # start time : 14:00:07 # end time : 14:02:14 ## This is the normal end. Don't worry. ## Start the postprocessor to look at the results. stop FDTDLoop
-general
infile= @last
-wakes
doit
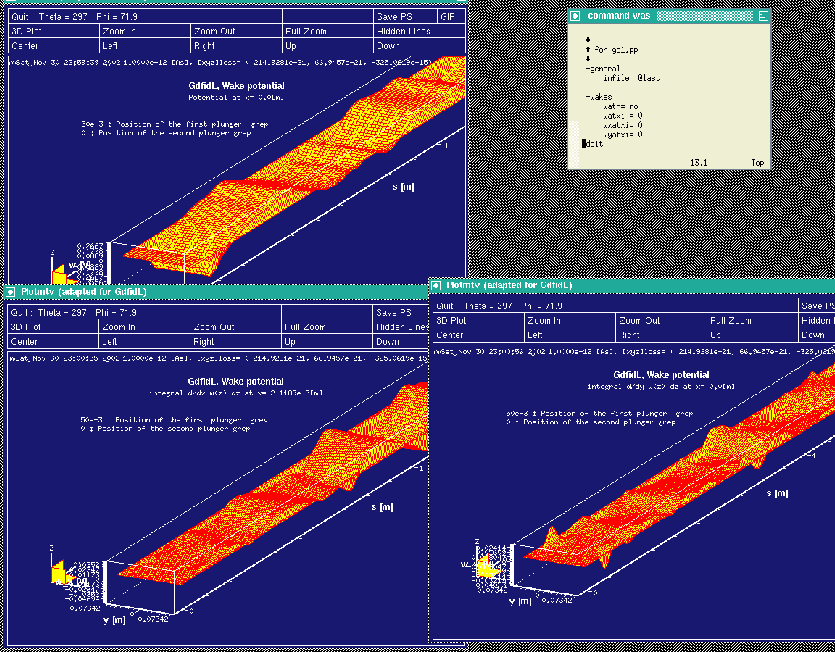
This is: We load the database of the last run, then we enter the section
-wakes and start the computation of the wake-potentials with the default
values.
gd1.pp then computes the wakepotentials from the data that were recorded by
gd1. gd1.pp starts three instances of mymtv2 to show the plots of the
computed longitudinal and transverse wakepotentials.
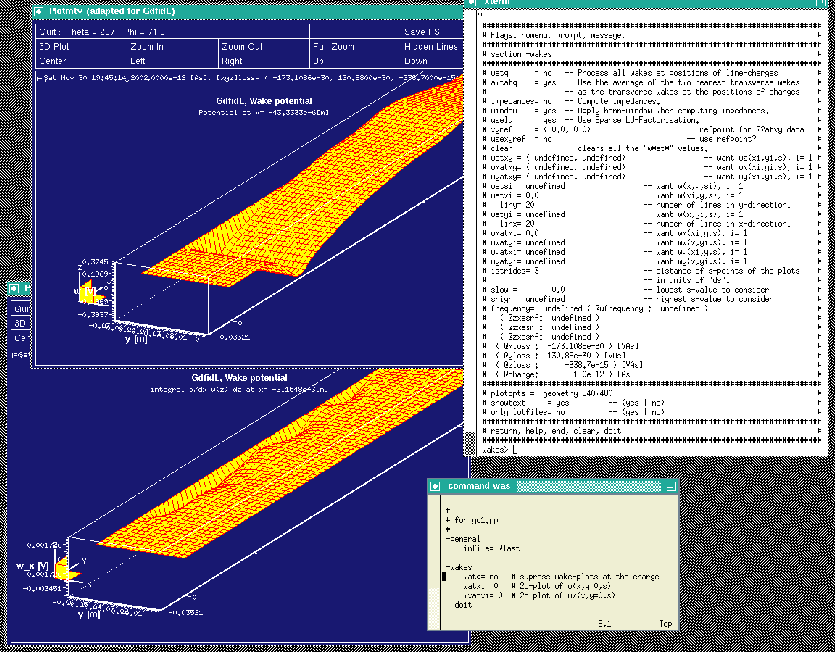
The resulting screen is shown in figure 4.1.
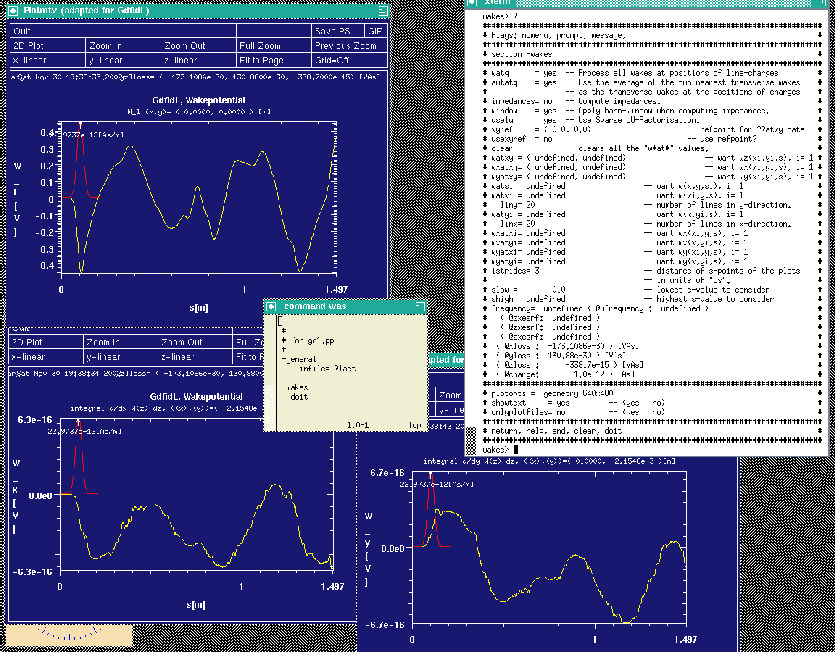 |
gd1.pp offers the choice to look at the longitudinal or transverse wakepotentials also as a function of (x,s) at a specified plane y=y0 or as a function of (y,s) at a specified plane x=x0.
We want to look at
watxi= 0 wxatxi= 0 doitThe resulting screen is shown in figure 4.2.
 |
-time
firstsaved= 0.1/@clight
lastsaved= 1/@clight
distancesaved= 0.1/@clight
in the inputfile for gd1, gd1 did save the electric and magnetic fields
at several times.
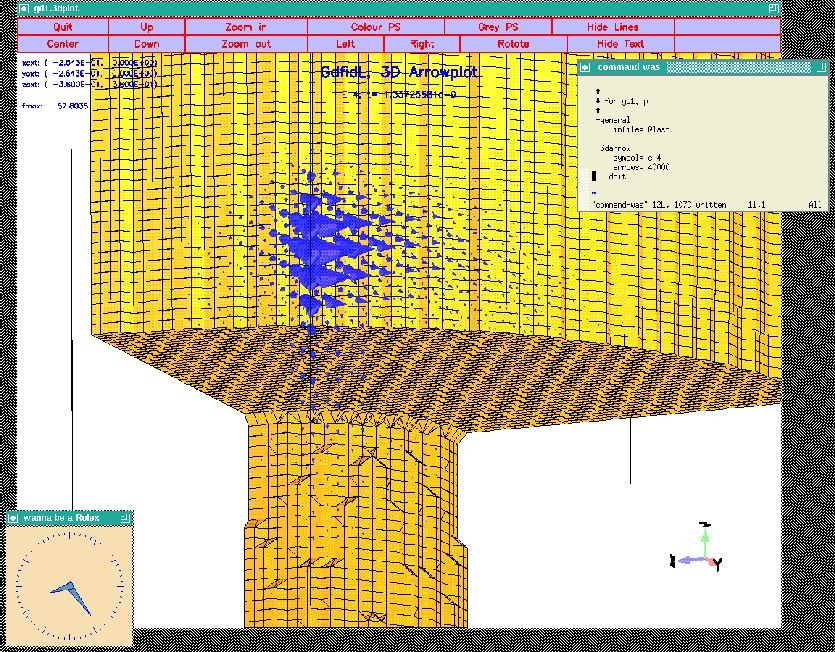
We look at the fourth saved electric field:
-3darrow
symbol= e_4
arrows= 40000 # default is 1000
# but for wakefields, better take more
doit
The resulting plot is shown in figure 4.3
 |
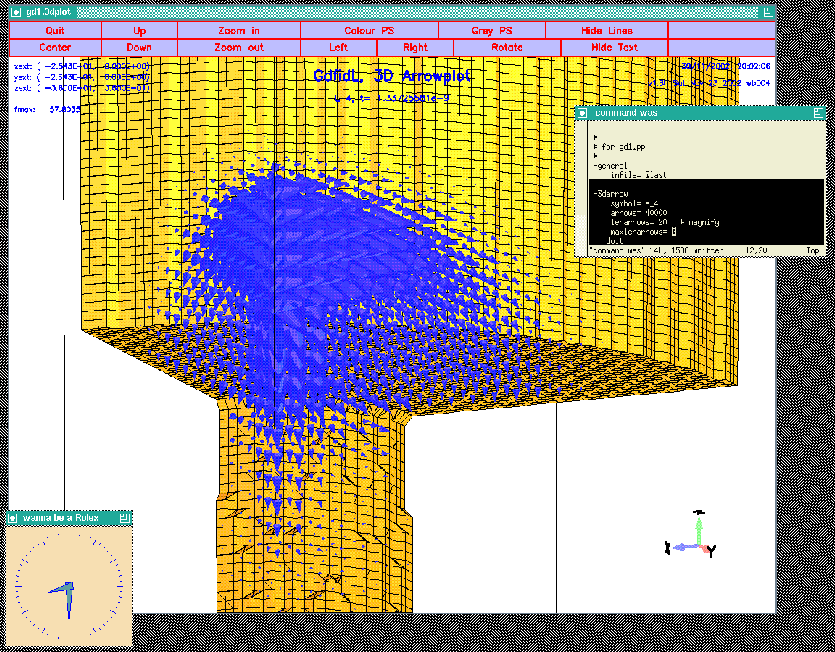
-3darrow
symbol= e_4
arrows= 40000 # default is 1000
# but for wakefields, better take more
lenarrows= 20 # <- magnify
maxlenarrows= 2 # .. but no arrow larger than "2"
doit
The resulting plot is shown in figure 4.4
 |
#
# a plunger
#
define(PlungerRadius0, 110e-3/2 )
define(PlungerInnerRadius, 100e-3/2 )
define(PlungerCurvature, 16e-3)
-gbor
material= 10
originprime= (0,0,0)
zprimedirection= (0,0,1)
rprimedirection= (1,0,0)
range= (0,360)
clear
# point= (z,r)
point= ( 0,0 )
point= ( 0, PlungerInnerRadius-PlungerCurvature )
arc, radius= PlungerCurvature, size= small, type= counterclockwise
point= ( -PlungerCurvature, PlungerInnerRadius )
point= ( -170e-3, PlungerInnerRadius )
point= ( -170e-3, 0 )
show= now,
doit
The figure 5.3 shows an outline of the body of revolution that
this decribes.
This plunger has its axis direction in z-direction.
Our plungers shall have their axis lying in the x-y-plane,
with an angle of -90+22.5 and 17 degrees.
In order to have the axis of our plunger direct in the proper direction, we
change the values of zprimedirection, rprimedirection.
These two vectors define the local z', r' coordinate-system, in which
the body of revolution is described.
We edit our inputfile:
define(PlungerAngle, (-90+22.5)*@pi/180 )
originprime= (0,0,0)
zprimedirection= ( -cos(PlungerAngle) ,\
-sin(PlungerAngle) ,\
0 )
rprimedirection= ( 0, 0, 1 )
The resulting outline is shown in figure 5.4.
We are not done yet: The plunger is not yet at the right position.
The origin of the plunger shall not be at (x,y,z)=(0,0,0), but at
(x,y,z)=(
define(PlungerRadius0, OuterRadius-50e-3 )
define(PlungerAngle, (-90+22.5)*@pi/180 )
originprime= ( cos(PlungerAngle)*PlungerRadius0 ,\
sin(PlungerAngle)*PlungerRadius0 ,\
0 )
zprimedirection= ( -cos(PlungerAngle) ,\
-sin(PlungerAngle) ,\
0 )
rprimedirection= ( 0, 0, 1 )
When we feed gd1 with this inputfile, we do not see the plunger in the
plot of the material-discretisation.
The reason is: The plunger is outside of the specified computational volume.
Since the geometry with the plunger does no longer have all three
symmetry-planes, we have to compute in a much larger volume.
The only symmetry plane left is the plane z=0.
So we change the specifications for the boundaries of the computational
volume to:
###
### We define the borders of the computational volume,
### we define the default mesh-spacing,
### and we define the conditions at the borders:
###
-mesh
spacing= InnerRadius/15
pxlow= -1.1*OuterRadius
pylow= -1.1*OuterRadius
pzlow = -(GapLength/2+TaperLength+9e-2)
pxhigh= 1.1*OuterRadius
pyhigh= 1.1*OuterRadius
pzhigh= 0
#
# The conditions to use at the borders of the computational volume:
#
cxlow= electric, cxhigh= electric
cylow= electric, cyhigh= electric
czlow= electric, czhigh= electric
The so edited inputfile can be found as
"/usr/local/gd1/Tutorial-SRRC/wPlunger00.gdf".
When we feed gd1 with this inputfile (gd1 macro.
Anywhere in an inputfile we can define macros.
A macro is enclosed between two lines: The first line contains the keyword
macro followed by the name of the macro.
All lines until a line with only the keyword endmacro are considered
the body of the macro.
When gd1 or gd1.pp find such a macro, they read it and store the body of the
macro in an internal buffer.
#
# This defines a macro with name 'foo'
#
macro foo
echo I am foo, my first argument is @arg1
echo The total number of arguments supplied is @nargs
endmacro
When gd1 or gd1.pp find a call of the macro, the number of the supplied
arguments is assigned to the variable @nargs, and the variables
@arg1, @arg2, .. are assigned the values of the supplied parameters
of the call.
The values of the arguments are strings. Of course it is possible
to have a string eg. '1e-4' which happens to be interpreted in the
right context as a real number.
# # this calls 'foo' with the arguments 'hi', 'there' # call foo(hi, there)Macro calls may be nested. The body of a macro may call another macro.
#
# a plunger
#
macro InnerPlunger
define(PlungerRadius0, @arg1 ) # Argument of the call
define(PlungerAngle, @arg2*@pi/180 ) # Argument of the call
define(PlungerInnerRadius, 100e-3/2 )
define(PlungerCurvature, 16e-3)
-gbor
material= 10
origin= ( cos(PlungerAngle)*PlungerRadius0 ,\
sin(PlungerAngle)*PlungerRadius0 ,\
0 )
zprimedirection= ( -cos(PlungerAngle)*PlungerRadius0 ,\
-sin(PlungerAngle)*PlungerRadius0 ,\
0 )
rprimedirection= (0,0,1)
range= (0,360)
clear
# point= (z,r)
point= (0,0)
point= (0, PlungerInnerRadius-PlungerCurvature )
arc, radius= PlungerCurvature, size= small, type= counterclockwise
point= ( -PlungerCurvature, PlungerInnerRadius )
point= ( -170e-3, PlungerInnerRadius )
point= ( -170e-3, 0)
doit
endmacro # InnerPlunger
macro OuterPlunger
define(PlungerOuterRadius, @arg1 )
define(PlungerAngle, (@arg2)*@pi/180 ) # Argument of the call
-gbor
material= 0
origin= ( cos(PlungerAngle)*OuterRadius,\
sin(PlungerAngle)*OuterRadius,\
0 )
zprimedirection= ( -cos(PlungerAngle),\
-sin(PlungerAngle),\
0 )
rprimedirection= (0,0,1)
range= (0,360)
clear
# point= (z,r)
point= ( 50e-3, 0 )
point= ( 50e-3, PlungerOuterRadius )
point= ( 50e-3, PlungerOuterRadius )
point= ( -235.39e-3, PlungerOuterRadius )
point= ( -235.39e-3, 50e-3)
point= ( -235.39e-3, 0)
doit
endmacro # OuterPlunger
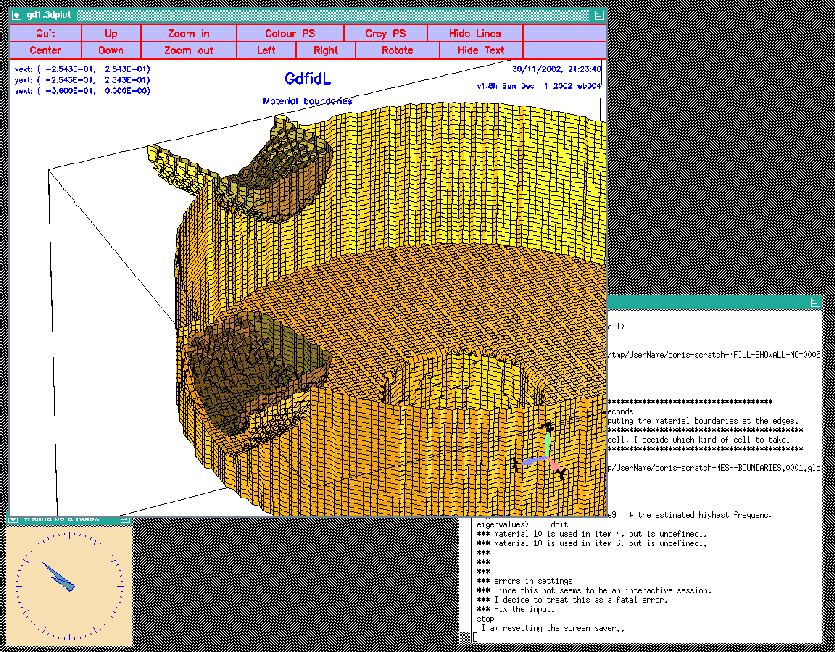
We now model each of our two plungers with two calls:
# # Model the tube and the plunger at phi=17 degrees: # call OuterPlunger( (130.75e-3/2) , 17 ) call InnerPlunger( (OuterRadius-50e-3), 17 ) # # model the tube and the plunger at phi=-90+22.5 degrees: # call OuterPlunger( (110e-3/2) , (-90+22.5) ) call InnerPlunger( (OuterRadius-50e-3), (-90+22.5) )The so edited inputfile can be found as /usr/local/gd1/Tutorial-SRRC/wPlunger01.gdf. When we feed gd1 with this inputfile, we get a screen as shown in figure 5.6.
 |
eigenvalues> solutions= 15 eigenvalues> estimation= 2e9 # the estimated highest frequency eigenvalues> doit *** material 10 is used in item 4, but is undefined.. *** material 10 is used in item 6, but is undefined.. *** errors in settings *** Since this not seems to be an interactive session, *** I decide to treat this as a fatal error. *** Fix the input. stopgd1 complains that we used a material index of '10' to model our plungers. The properties of this material '10' have not yet been defined. We doit by editing our inputfile, such that before the eigenvalue computation starts, we have:
-material # enter the section "-material"
material= 10 # the properties of material "10" shall be changed.
type= electric # shall be treated as perfect electric conducting
# for the field computation
We did use the materials '0' and '1' as well. We did not define the
properties of them, but the default values of these materials are what we want
(material '0' is vacuum, material '1' is copper, and material '2' is perfect
magnetic conducting).
boundary conditions:
xboundary= electric, electric
yboundary= electric, electric
zboundary= electric, electric
--------------------
i freq(i) acc(i) cont(i)
1 436.4010e+6 1.0044982017 1.0000000000 # "grep" for me
2 508.3705e+6 0.0014197280 0.0014201239 # "grep" for me
3 782.2763e+6 0.0000381458 0.0000535041 # "grep" for me
4 785.5885e+6 0.0002404450 0.0003882672 # "grep" for me
5 1.0476e+9 0.0000318869 0.0000629098 # "grep" for me
6 1.0620e+9 0.0002907024 0.0049598724 # "grep" for me
7 1.0930e+9 0.0002534295 0.0044621769 # "grep" for me
8 1.0985e+9 0.0001211415 0.0014816978 # "grep" for me
9 1.1436e+9 0.0003028035 0.0023958708 # "grep" for me
10 1.2149e+9 0.0040771062 0.0350091443 # "grep" for me
11 1.2437e+9 0.0074278316 0.1613287149 # "grep" for me
12 1.2652e+9 0.0671920760 1.0000000000 # "grep" for me
13 1.2845e+9 0.0265391147 0.5529007301 # "grep" for me
14 1.3151e+9 0.0376288530 0.3142827624 # "grep" for me
15 1.3935e+9 0.0930865808 0.8046319226 # "grep" for me
################################
# cpu-seconds for eigenvalues : 472
# start date : 30/11/2002
# end date : 30/11/2002
# start time : 21:41:36
# end time : 21:50:45
# The computation of the eigenvalues has finished normally..
# Start the postprocessor to look at the results.
stop .. normal end ..
The first mode is garbage, as can be seen from its accuracy.
But also the other modes are not very good.
The reason is: Since we have only a single symmetry plane left (z=0),
we have to compute in a volume that is four times as large as the volume
before. In such a large volume, there are much more modes than 15 in the
frequency range from 0 to estimation (we specified
an estimation of 2GHz).
We could say that we want to have more solutions, but that would
drastically increases our memory consumption.
Since we are using already about 200 MBytes
(our grid contains 1.2 million gridcells), we do not want to do this.
We could try to compute with the single precision version of
gd1, single.gd1, then we could compute 30 modes in 200 MByte.
Instead we adjust our estimation to 1.2 GHz.
The end of our inputfile now is:
-eigenvalues
solutions= 15
estimation= 1.2e9 # the estimated highest frequency
doit
and the final table of a run (gd1
boundary conditions:
xboundary= electric, electric
yboundary= electric, electric
zboundary= electric, electric
--------------------
The first 2 solutions seem to be static and are not saved.
i freq(i) acc(i) cont(i)
1 508.3705e+6 0.0000027120 0.0000022258 # "grep" for me
2 782.2764e+6 0.0000000527 0.0000000740 # "grep" for me
3 785.5885e+6 0.0000000113 0.0000000182 # "grep" for me
4 1.0476e+9 0.0000000021 0.0000000042 # "grep" for me
5 1.0620e+9 0.0000000009 0.0000000155 # "grep" for me
6 1.0930e+9 0.0000000245 0.0000004322 # "grep" for me
7 1.0985e+9 0.0000000053 0.0000000651 # "grep" for me
8 1.1436e+9 0.0000000643 0.0000005090 # "grep" for me
9 1.2149e+9 0.0000675156 0.0005797832 # "grep" for me
10 1.2434e+9 0.0000015519 0.0000339391 # "grep" for me
11 1.2587e+9 0.0000055368 0.0001618450 # "grep" for me
12 1.2801e+9 0.0006670306 0.0200800431 # "grep" for me
13 1.2994e+9 0.0015633650 0.0522703164 # "grep" for me
################################
# cpu-seconds for eigenvalues : 747
# start date : 30/11/2002
# end date : 30/11/2002
# start time : 21:52:37
# end time : 22:06:21
# The computation of the eigenvalues has finished normally..
# Start the postprocessor to look at the results.
stop .. normal end ..
The garbage mode has disappeared, and the accuracies the modes are very good.
![[*]](crossref.png) to
compute the variation of the accelerating voltage as a function of the
x-position.
For convenience, the shell script '/usr/local/gd1/Tutorial-SRRC/x-voltages.x'
is shown here again:
to
compute the variation of the accelerating voltage as a function of the
x-position.
For convenience, the shell script '/usr/local/gd1/Tutorial-SRRC/x-voltages.x'
is shown here again:
#!/bin/sh
#
# feed the postprocessor with a 'here'-document,
# 'tee' the output of the postprocessor to the file "pp.out"
#
(gd1.pp | tee pp.out) << EOF
nomenu, noprompt, nomessage # no unneccessary output
-general, infile= @last
-lintegral
symbol= e_1
direction= z, component= z
do ix= 1, @nx
startpoint= ( @x(ix), 0, @zmin )
doit
echo @x0 @vreal @vimag # <= x, vreal, vimag
enddo
end
EOF
#
# Write a PlotMtv-header to "x-voltages.mtv".
#
# Process the file "pp.out":
# 'grep' the lines with the pattern "vreal"
#
echo \$ DATA= COLUMN > x-voltages.mtv
echo x vreal vimag >> x-voltages.mtv
grep vreal pp.out >> x-voltages.mtv
#
# now start "mymtv2" to display the data:
#
mymtv2 -mult -landscape x-voltages.mtv
The resulting plot is shown in figure 7.1.
 |
-Dname=value when starting
the program.
gd1 then defines a symbolic variable with name name to have the
value value.
The effect is therefore the same as if in the very first line of its input,
the line sdefine(name, value) would occur.
We write a small shell script that starts gd1 three times with three
different values for the option.
#!/bin/sh
for POS1 in 0e-3 25e-3 50e-3
do
gd1 -Dposition1=$POS1 -Dposition2=0 \
< /usr/local/gd1/Tutorial-SRRC/wPlunger04.gdf | tee out.pos1=$POS1
done
This shell-script can be found as '/usr/local/gd1/Tutorial-SRRC/many-pos1.x'.
The inputfile 'wPlunger04.gdf' now calls the macros as follows:
# # Model the tube and the plunger at phi=17 degrees: # call OuterPlunger( (130.75e-3/2) , 17 ) call InnerPlunger( (OuterRadius-position1), 17 ) # # model the tube and the plunger at phi=-90+22.5 degrees: # call OuterPlunger( (110e-3/2) , (-90+22.5) ) call InnerPlunger( (OuterRadius-position2), (-90+22.5) )The actual positions are output as annotations by specifying in the section
-general:
-general
text()= position1 : Position of the first plunger grep
text()= position2 : Position of the second plunger grep
When gd1 reads this, it will substitute the 'position1' with the value
that was supplied to it via its commandline option -Dposition1=$POS1,
the corresponding happens to the string 'position2'.
The strings 'grep' are supplied so that the outputfiles out.pos1=$POS1
can be 'grep'ed for the string 'grep'.
The full inputfile can be found as
/usr/local/gd1/Tutorial-SRRC/wPlunger04.gdf'.
When we run our shell script, we get three files
out.pos1=0e-3, out.pos1=25e-3, out.pos1=50e-3where the computed frequencies can be found in. The relevant lines can be easily extracted with the UNIX-command 'grep'. To show all lines in the files
out.pos* that contain the string 'grep',
you say
grep grep out.pos*The result is:
out.pos1=0e-3: general> text()= 0e-3 : Position of the first plunger grep out.pos1=0e-3: general> text()= 0 : Position of the second plunger grep Position of the first plunger: 0e-3 grep Position of the second plunger: 0 grep out.pos1=0e-3: 1 52.7470e+06 1.0090174050 0.3438316719 # "grep" for me out.pos1=0e-3: 2 502.5682e+06 0.0000031370 0.0000025505 # "grep" for me out.pos1=0e-3: 3 778.1484e+06 0.0000000660 0.0000000914 # "grep" for me out.pos1=0e-3: 4 779.3503e+06 0.0000000163 0.0000000249 # "grep" for me out.pos1=0e-3: 5 1.0554e+09 0.0000000001 0.0000000002 # "grep" for me out.pos1=0e-3: 6 1.0591e+09 0.0000000003 0.0000000045 # "grep" for me out.pos1=0e-3: 7 1.0971e+09 0.0000000012 0.0000000173 # "grep" for me out.pos1=0e-3: 8 1.0973e+09 0.0000000045 0.0000000428 # "grep" for me out.pos1=0e-3: 9 1.1560e+09 0.0000000521 0.0000005213 # "grep" for me out.pos1=0e-3: 10 1.1976e+09 0.0000001260 0.0000013792 # "grep" for me out.pos1=0e-3: 11 1.2515e+09 0.0004255555 0.0049426207 # "grep" for me out.pos1=0e-3: 12 1.2656e+09 0.0016319888 0.0731105041 # "grep" for me out.pos1=0e-3: 13 1.2668e+09 0.0025985547 1.0000000000 # "grep" for me out.pos1=25e-3: general> text()= 25e-3 : Position of the first plunger grep out.pos1=25e-3: general> text()= 0 : Position of the second plunger grep out.pos1=25e-3: 25e-3 : Position of the first plunger grep out.pos1=25e-3: 0 : Position of the second plunger grep out.pos1=25e-3: 1 503.7682e+06 0.0000024488 0.0000019899 # "grep" for me out.pos1=25e-3: 2 779.4209e+06 0.0000000124 0.0000000171 # "grep" for me out.pos1=25e-3: 3 781.0514e+06 0.0000000431 0.0000000660 # "grep" for me out.pos1=25e-3: 4 1.0575e+09 0.0000000027 0.0000000051 # "grep" for me out.pos1=25e-3: 5 1.0595e+09 0.0000000002 0.0000000024 # "grep" for me out.pos1=25e-3: 6 1.0968e+09 0.0000000062 0.0000000913 # "grep" for me out.pos1=25e-3: 7 1.0975e+09 0.0000000018 0.0000000174 # "grep" for me out.pos1=25e-3: 8 1.1555e+09 0.0000000372 0.0000003780 # "grep" for me out.pos1=25e-3: 9 1.2018e+09 0.0000002208 0.0000025548 # "grep" for me out.pos1=25e-3: 10 1.2529e+09 0.0007020442 0.0086314595 # "grep" for me out.pos1=25e-3: 11 1.2675e+09 0.0009580488 0.0414770393 # "grep" for me out.pos1=25e-3: 12 1.2746e+09 0.0020655866 0.1865897939 # "grep" for me out.pos1=50e-3: general> text()= 50e-3 : Position of the first plunger grep out.pos1=50e-3: general> text()= 0 : Position of the second plunger grep out.pos1=50e-3: 50e-3 : Position of the first plunger grep out.pos1=50e-3: 0 : Position of the second plunger grep out.pos1=50e-3: 1 99.6144e+06 0.9656790469 0.3479304400 # "grep" for me out.pos1=50e-3: 2 505.2467e+06 0.0000031189 0.0000025741 # "grep" for me out.pos1=50e-3: 3 779.6769e+06 0.0000000046 0.0000000065 # "grep" for me out.pos1=50e-3: 4 781.9646e+06 0.0000000537 0.0000000853 # "grep" for me out.pos1=50e-3: 5 1.0479e+09 0.0000000086 0.0000000166 # "grep" for me out.pos1=50e-3: 6 1.0605e+09 0.0000000016 0.0000000236 # "grep" for me out.pos1=50e-3: 7 1.0955e+09 0.0000000193 0.0000003011 # "grep" for me out.pos1=50e-3: 8 1.0983e+09 0.0000000036 0.0000000400 # "grep" for me out.pos1=50e-3: 9 1.1477e+09 0.0000000200 0.0000001945 # "grep" for me out.pos1=50e-3: 10 1.2055e+09 0.0000001903 0.0000020180 # "grep" for me out.pos1=50e-3: 11 1.2473e+09 0.0031135695 0.0463915760 # "grep" for me out.pos1=50e-3: 12 1.2570e+09 0.0168888927 0.6785522929 # "grep" for me out.pos1=50e-3: 13 1.2726e+09 0.0118906521 0.4821503838 # "grep" for meThis usage of gd1 is the reason, why gd1 writes the string
"grep" for mein the table of the frequencies.
###
### We define the borders of the computational volume,
### we define the default mesh-spacing,
### and we define the conditions at the borders:
###
-mesh
spacing= InnerRadius/15
pxlow= -1.1*OuterRadius
pylow= -1.1*OuterRadius
pzlow = -(GapLength/2+TaperLength+9e-2)
pxhigh= 1.1*OuterRadius
pyhigh= 1.1*OuterRadius
pzhigh= (GapLength/2+TaperLength+9e-2)
#
# The conditions to use at the borders of the computational volume:
#
cxlow= electric, cxhigh= electric
cylow= electric, cyhigh= electric
czlow= electric, czhigh= electric
For the linecharge, we have to specify its total charge, its length,
and the (x,y)-position where it shall travel.
We also have to say that we do not want to compute eigenvalues, but we want to
perform a time domain computation.
We specify that at the lower and upper z-planes absorbing boundary
conditions shall be applied.
In the section -time, we specify that we want to have saved
the fields at 10 equidistant times between the time that the line charge
has traveled 0.1 m and it has traveled 1 m.
We edit our inputfile, such that the end of it looks as:
-eigenvalues
solutions= 15
estimation= 2e9 # the estimated highest frequency
# doit
-fdtd
-lcharge
charge= 1e-12
sigma= 4*STPSZE
xposition= 0, yposition= 0
shigh= 1.5
showdata= yes
-ports
name= beamlow , plane= zlow, modes= 3, npml= 40, doit
name= beamhigh, plane= zhigh, modes= 3, npml= 40, doit
-time
firstsaved= 0.1/@clight
lastsaved= 1/@clight
distancesaved= 0.1/@clight
-fdtd
doit
The so edited inputfile can be found as
/usr/local/gd1/Tutorial-SRRC/wPlunger-wake.gdf.
When we feed gd1 with the edited inputfile,
gd1 < wPlunger-wake.gdfgd1 stops and complains
# was: " call InnerPlunger( (OuterRadius-position1), 17 )"
gbor>
gbor> *** rnum: Bad Constant: starts here: "position1) "
evaluate me(:lenEvaluate): "(231.15e-3-position1) "
*** Status: "Bad factor :"p""
*** : "(231.15e-3-position1) "
|
*** Since this not seems to be an interactive session,
*** I decide to treat this as a fatal error.
*** Fix the input.
stop
We did not specify what the value of the symbols position1 and
position2 shall be.
We do this by defining them on the commandline of gd1:
gd1 -Dposition1=50e-3 -Dposition2=0 < wPlunger-wake.gdfNow the computation runs. After some minutes, the last words of gd1 are:
timestep= 900, simulated time= 6.9214e-9 s wakepotentials are known up to s= 1.3455 m cpu time/sec: used: 300.13, since last call: 31.23, MFLOPs/s: 82.67 Wall clock time: 305.99 s, MFLOPs/s: 81.09 The highest simulation time is reached .., I am stopping ################################ # cpu-seconds for FDTD : 320 # start date : 30/11/2002 # end date : 30/11/2002 # start time : 22:25:31 # end time : 22:33:22 ## This is the normal end. Don't worry. ## Start the postprocessor to look at the results. stop FDTDLoop
-general
infile= @last
-3darrow
symbol= e_4
arrows= 40000
doit
The resulting screen is shown in figure 10.1.
 |
-3darrowplot. With this option
we can switch on or off the plotting of the material boundaries:
materials= yes|no.
The default value is materials= yes.
We select
materials= no doitNow we see the field, but no material anywhere. The resulting plot is shown in figure 10.2.
 |
materials= yes bbzhigh= 0 # don't plot anything above z=0The resulting plot is shown in figure 10.3.
 |
-wakes. When we are solely interested in the
longitudinal and transverse wakepotentials at the position
of the line-charge, we do not have to specify any special option,
the default values are good for that.
The default is to compute and plot the longitudinal and transverse
wakepotentials at the position of the exciting charge.
We say
-wakes
doit
The resulting plots are shown in figure 10.4.
 |
watsi= 0.9 watsi= 1.1 watq= no doitthe
watq= no
instructs gd1.pp that we do not want to see again the
wakepotentials at the position of the linecharge.
We did specify watsi= ?? twice, this means, that we want to see
the wakepotential at both s-coordinates.
The resulting plots are shown in figure 10.5.
 |
watxi = 0 wxatxi= 0 wyatxi= 0 watyi = 0 wxatyi= 0 wyatyi= 0 doitThe resulting plots are shown in the figures 10.6 and 10.7
 |
 |
This is the end of this tutorial.