next_inactive up previous


How to model the BESSY cavity with GdfidL v1

Warner Bruns

November 14, 2003

\psfig{figure=bessy.perfect.PS,width=12cm,bbllx=109pt,bblly=93pt,bburx=596pt,bbury=423pt,clip=}

Contents


List of Figures

  1. Screenshot of a typical desktop when one uses gd1. The xterm in the upper right corner is used to edit the inputfile, the xterm in the lower right is used to feed gd1 with the inputfile, and the long xterm on the right side runs another instance of gd1. This second instance of gd1 is used to look-up the syntax of gd1's command language.
  2. A scetch of the cavity with attached HOM-coupler.
  3. Screenshot of the desktop when the inputfile bessy00.gdf has been fed into gd1. gd1 has popped up an instance of mymtv2 that shows the outline of the specified polygon.
  4. Screenshot of the desktop when the inputfile bessy01.gdf has been fed into gd1. gd1 has popped up an instance of gd1.3dplot that shows the generated mesh.
  5. A cross-section of the attached waveguides.
  6. An outline of the general cylinder that shall decribe the waveguide.
  7. The waveguide now has its axis showing in the right direction.
  8. The radius of the waveguide and the gap of the ridge as a function of the position within the waveguide.
  9. Screenshot with the outline as produced by calling the macro 'Linear_Waveguide' three times with different parameters. In the background, an example of a generated mesh is shown.
  10. Screenshot with the outline as produced by calling the macros 'Linear_waveguide' and 'Linear_Ridge' three times with different parameters. In the background, an example of a generated mesh is shown.
  11. Screenshot with the outline as produced by the many calls of the macros. In the background, an example of a generated mesh is shown.
  12. An outline of the general cylinder that shall decribe a transformer.
  13. Screenshot with the outline as produced by the many calls of the macros. In the background, an example of a generated mesh is shown. The used inputfile can be found as 'almost-done.gdf'.

What this paper contains

We got detailed technical data1 of the proposed BESSY cavity.

The technical data are transformed step by step into an inputfile for gd1. Every step is explained in detail. Numerous hints are given, how one effectively models the geometry.

Modeling the rotational symmetric part of the cavity

Meshing

Recommended usage of gd1

The most effective usage of gd1 is: If you work with several xterms, this cycle is very fast. Figure 1.1 shows a typical ``desktop`` with three xterms. The upper right xterm is a terminal running an editor to change the inputfile, the lower right xterm is used to feed gd1 with the actual inputfile, and a third xterm is used to run another instance of gd1. This second instance of gd1 is used to look-up the syntax of gd1's commands.

Figure 1.1: Screenshot of a typical desktop when one uses gd1. The xterm in the upper right corner is used to edit the inputfile, the xterm in the lower right is used to feed gd1 with the inputfile, and the long xterm on the right side runs another instance of gd1. This second instance of gd1 is used to look-up the syntax of gd1's command language.
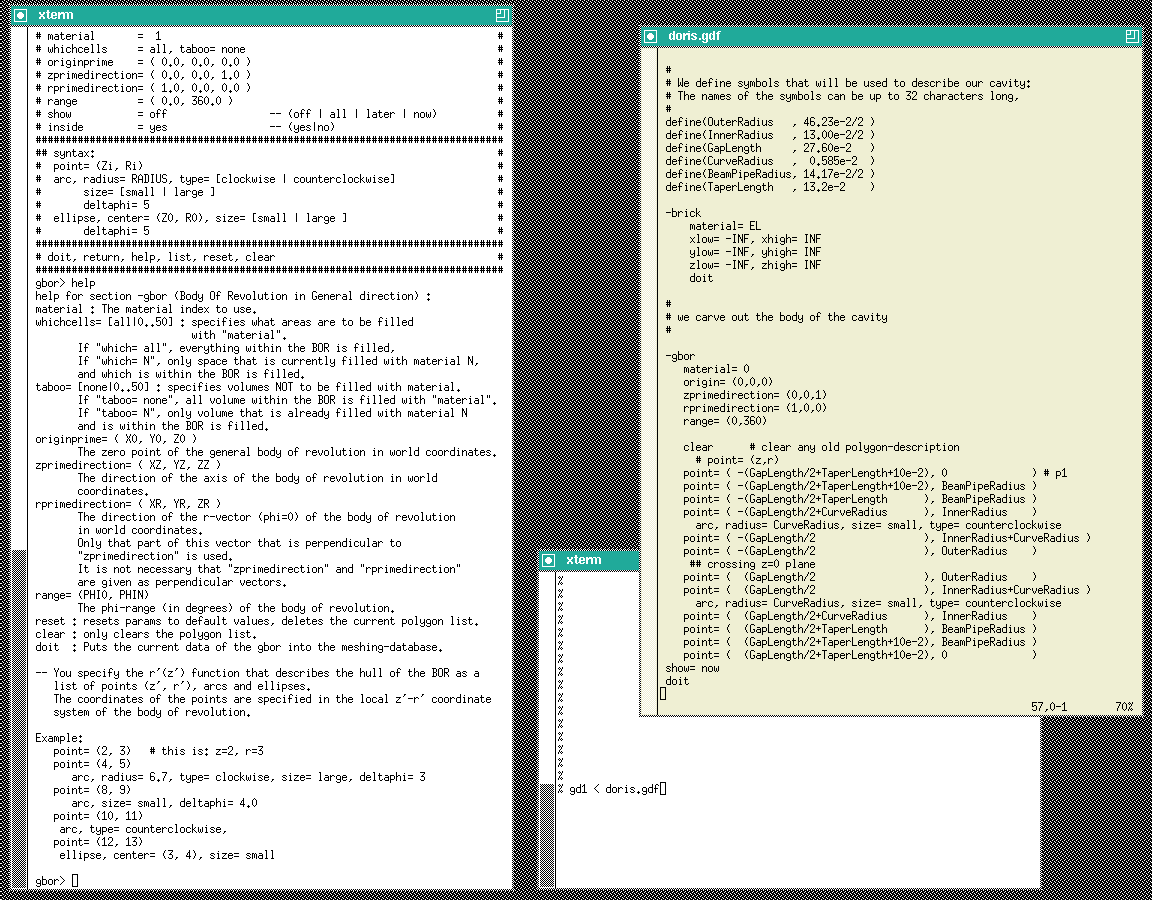\begin{figure}\begin{center}\psfig{figure=dumped00.PS,width=723.0pt} \end{center} \end{figure}

Modelling the geometry

The cavity we want to analyse is essentially a body of revolution. There are three higher order mode (HOM) couplers attached. The hard to model part are the HOM-couplers.

Figure 1.2: A scetch of the cavity with attached HOM-coupler.
\begin{figure}\centerline{ \psfig{figure=scanned/w2.PS,width=12cm} }\end{figure}

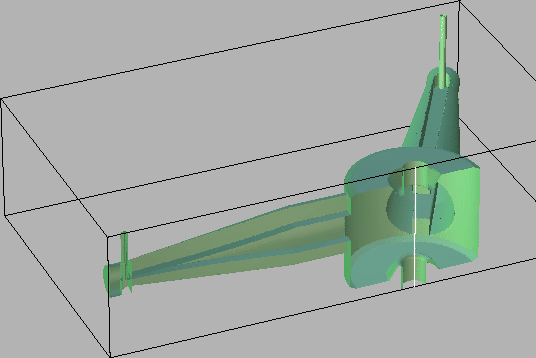
In the first step we model the cavity and the beam-pipes. We do this by specifying a polygonal description of the boundary in the r-z-plane. The inputfile that describes the boundary is: 

 #
 # Some helpful symbols:
 #
 define(EL, 1) define(MAG, 2)
 define(INF, 1000)

 #
 # We define symbols that will be used to describe our cavity:
 # The names of the symbols can be up to 32 characters long,
 #
 define(OuterRadius   , 46.23e-2/2 )
 define(InnerRadius   , 13.00e-2/2 )
 define(GapLength     , 27.60e-2   )
 define(CurveRadius   ,  0.585e-2  )
 define(BeamPipeRadius, 14.17e-2/2 )
 define(TaperLength   , 13.2e-2    )

 ########
 #
 # We fill the universe with metal
 #
 -brick
     material= EL
     xlow= -INF, xhigh= INF
     ylow= -INF, yhigh= INF
     zlow= -INF, zhigh= INF
     doit
 
 #
 # we carve out the body of the cavity
 #

 -gbor
    material= 0
    origin= (0,0,0)
    range= (0,360)

    clear
      #
      # the following polygon describes the upper part of the cavity:
      #
      point= ( -1e-6, 0) # (z,r)
      point= ( 0.1+0.27, 0)
      point= ( 0.1+0.27, 0.037 )
      point= ( 0.126, 0.037)
        arc, radius= 0.01, size= small, type= clockwise
      point= ( 0.116, 0.047)
        arc,
      point= ( 0.1207008, 0.0554805 )
      point= ( 0.1595, 0.0797249 )
      point= ( 0.1595, 0.1836 )
      point= ( 0.1495, 0.2027 ) # 0.2027 am 7.ten November 2003
      point= ( 0, 0.2027 )
      point= ( -1e-6, 0 )

      #
      # specify the r- and z-direction of the BOR,
      # model the upper part.
      #
    rprime= ( 1, 0, 0 )
    zprime= ( 0, 0, 1 ) # Upper part of the cavity
    show= later
    doit

      #
      # re-specify the z-direction,
      # model the lower part.
      #
    zprime= ( 0, 0, -1 ) # lower part of the cavity
    show= all
    doit

 -volumeplot
    doit
This inputfile can be found as "/usr/local/gd1/Tutorial-Bessy/bessy00.gdf". When we feed this file into gd1 via the command "gd1 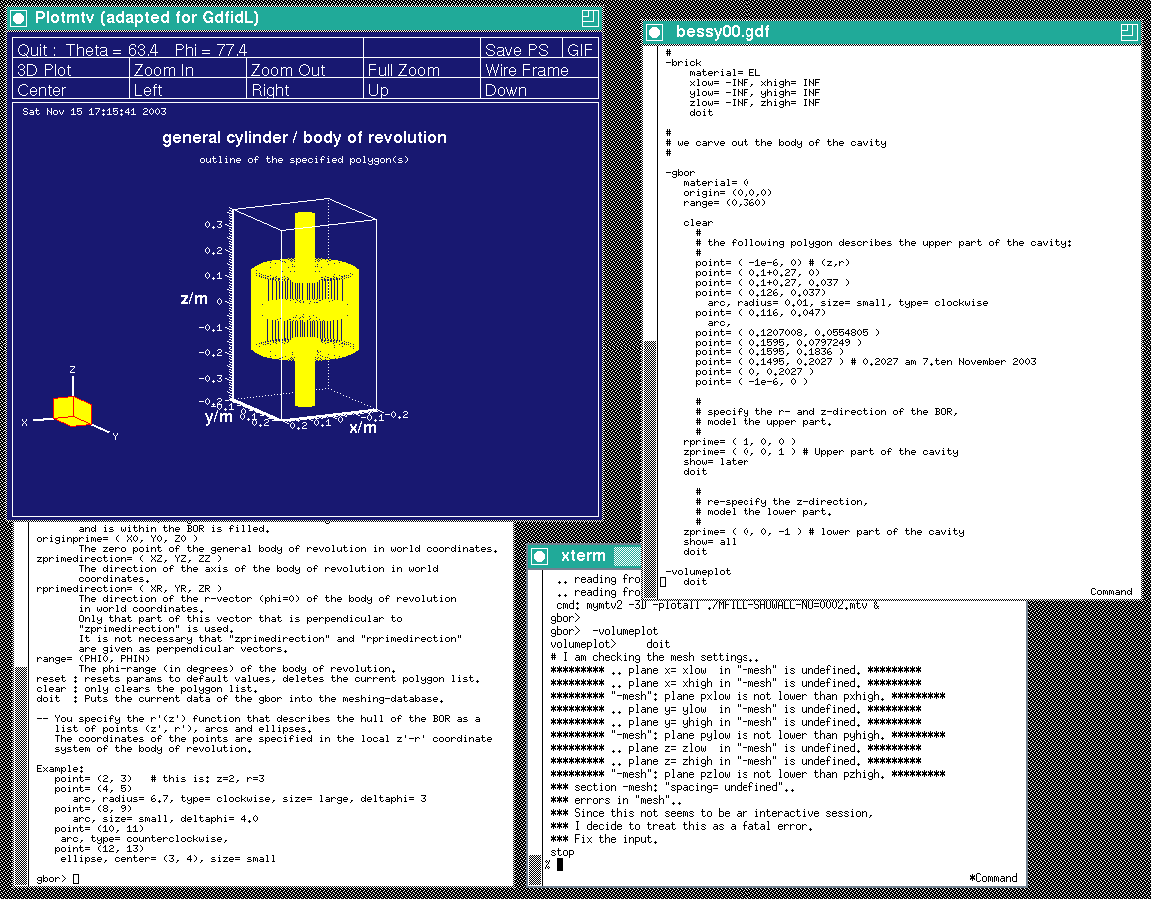$<$ bessy00.gdf", we get a desktop similiar to the one shown in figure 1.3
Figure 1.3: Screenshot of the desktop when the inputfile bessy00.gdf has been fed into gd1. gd1 has popped up an instance of mymtv2 that shows the outline of the specified polygon.
\begin{figure}\centerline{ \psfig{figure=bessy00.PS,width=723.0pt} }\end{figure}

gd1 does not what we want, we do not get a "volumeplot", although we requested one. But gd1 gives us a hint what we made wrong: 

 gbor>  -volumeplot
 volumeplot>     doit
 # I am checking the mesh settings..
 ********* .. plane x= xlow  in "-mesh" is undefined. *********
 ********* .. plane x= xhigh in "-mesh" is undefined. *********
 ********* "-mesh": plane pxlow is not lower than pxhigh. *********
 ********* .. plane y= ylow  in "-mesh" is undefined. *********
 ********* .. plane y= yhigh in "-mesh" is undefined. *********
 ********* "-mesh": plane pylow is not lower than pyhigh. *********
 ********* .. plane z= zlow  in "-mesh" is undefined. *********
 ********* .. plane z= zhigh in "-mesh" is undefined. *********
 ********* "-mesh": plane pzlow is not lower than pzhigh. *********
 *** section -mesh: "spacing= undefined"..
 *** errors in "mesh"..
 *** Since this not seems to be an interactive session,
 *** I decide to treat this as a fatal error.
 *** Fix the input.
 stop
When we say "doit" in the section "-volumeplot", gd1 tries to generate the mesh. But in order to generate the mesh, gd1 needs to know All these informations have to be given to gd1 before a volumeplot is requested. Since gd1 has detected that it is fed by an inputfile and is not used interactively, it stops as soon some essential information is not available. When not run interactively, gd1 also stops when some syntax error is present in the inputfile.

To give gd1 the needed information, we change our inputfile. We insert the following lines somewhere before "-volumeplot": 

 ###
 ### We define the borders of the computational volume,
 ### and we define the default mesh-spacing.
 ###
 -mesh
     spacing= InnerRadius/15
     pxlow= -1.1*OuterRadius, pxhigh= 1.1*OuterRadius
     pylow= -1.1*OuterRadius, pyhigh= 1.1*OuterRadius
     pzlow = -(GapLength/2+TaperLength+9e-2)
     pzhigh= +(GapLength/2+TaperLength+9e-2)
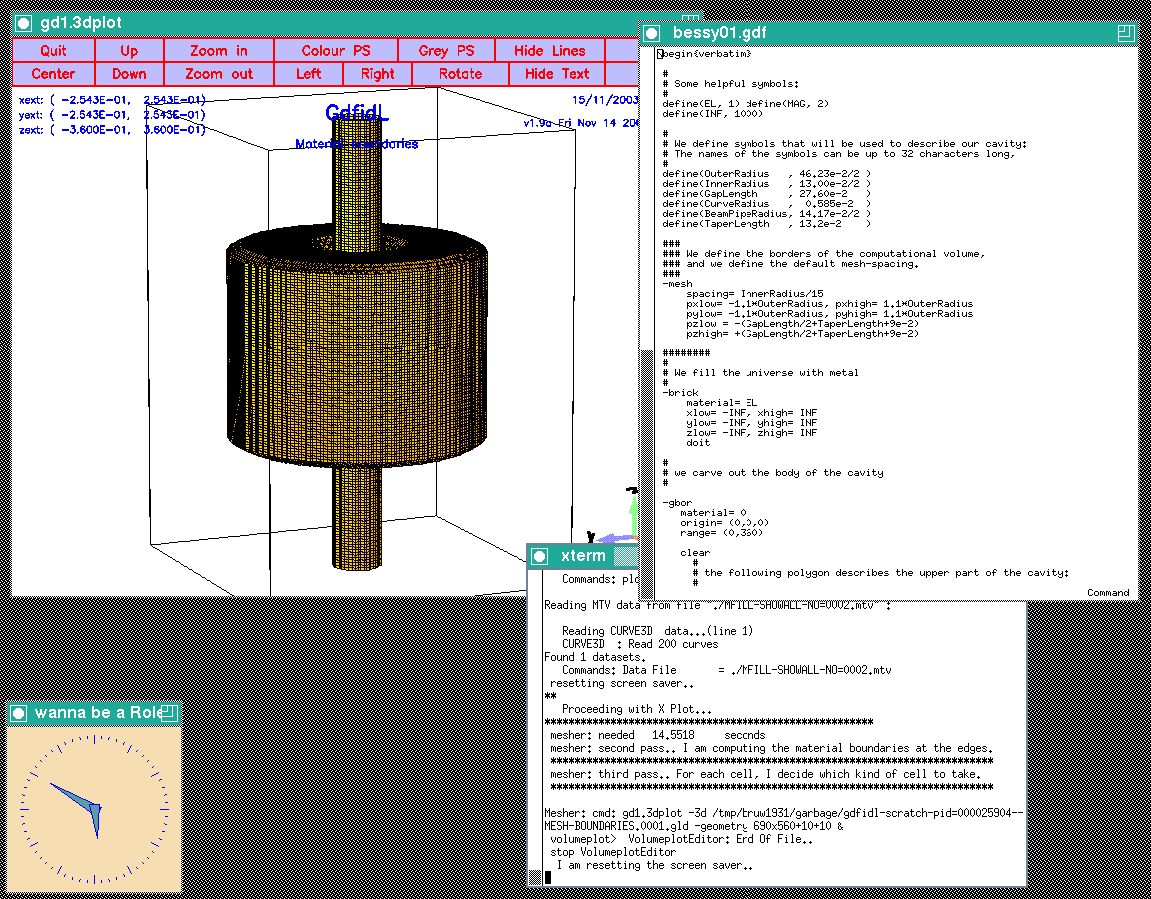
The so edited inputfile can be found as "/usr/local/gd1/Tutorial-Bessy/bessy01.gdf".

When we feed gd1 with this inputfile (gd1 $<$ bessy01.gdf) we get a screen similiar to the one shown in figure 1.4

Figure 1.4: Screenshot of the desktop when the inputfile bessy01.gdf has been fed into gd1. gd1 has popped up an instance of gd1.3dplot that shows the generated mesh.
\begin{figure}\centerline{ \psfig{figure=bessy01.PS,width=723.0pt} }\end{figure}

Modelling the real 3D geometry

The real geometry has three higher oder mode (HOM) couplers attached. The couplers consist of a hollow waveguide section and a hollow waveguide to coaxial waveguide adapter. The coaxial waveguide is terminated by a matched load.

The hollow waveguide section is a ridged waveguide where the cross section varies continously. The waveguide is designed such, that at every cross section the cutoff frequency of the fundamental mode is the same.

Modelling a straight waveguide attached under an arbitrary angle

Figure 1.5: A cross-section of the attached waveguides.
\begin{figure}\centerline{ \psfig{figure=scanned/cross-section.PS,width=12cm} }\end{figure}

Figure 1.6: An outline of the general cylinder that shall decribe the waveguide.
\begin{figure}\centerline{ \psfig{figure=waveguide00.PS,width=14cm,bbllx=1pt,bblly=1pt,bburx=529pt,bbury=775pt,clip=} }\end{figure}
The waveguides a general cylinders, where the cross section of the cylinders is some polygon. gd1 can model this directly. We edit our inputfile so that it contains: 
 define(GuideR0, 200e-3/2)
 define(GuideGap, 42.548e-3)
 define(WW, 51e-3)
 define(RR2, 2e-3)
 define(RR5, 5e-3)

 -ggcylinder
    material= 0
    range= ( 0, 100e-3 )

 define(AA, WW/2+RR5)
 define(BB, ((GuideR0-RR5)**2 - AA**2)**0.5)
 define(THETA, atan2(BB, AA))

    clear

       # +x, +y
       point= ( GuideR0, 0 ) # x', y'
          arc, radius= GuideR0, size= small, type= counterclockwise, deltaphi= 5
       point= ( GuideR0*cos(THETA), GuideR0*sin(THETA) )
          arc, radius= RR5, size= small, type= counterclockwise, , deltaphi= 15
       point= (  WW/2   , BB )
       point= (  WW/2   , GuideGap/2+ RR2 )
          arc, radius= RR2, size= small, type= clockwise
       point= (  WW/2-RR2 , GuideGap/2 )

       # -x, +y
       point= ( -(WW/2-RR2), GuideGap/2 )
          arc, radius= RR2, size= small, type= clockwise
       point= ( -WW/2   , GuideGap/2+ RR2 )
       point= ( -WW/2   , BB )
          arc, radius= RR5, size= small, type= counterclockwise, , deltaphi= 15
       point= ( -GuideR0*cos(THETA), GuideR0*sin(THETA) )
          arc, radius= GuideR0, size= small, type= counterclockwise, deltaphi= 5
       point= ( -GuideR0, 0 ) # x', y'

       # -x, -y
       point= ( -GuideR0, 0 ) # x', y'
          arc, radius= GuideR0, size= small, type= counterclockwise, deltaphi= 5
       point= ( -GuideR0*cos(THETA), -GuideR0*sin(THETA) )
          arc, radius= RR5, size= small, type= counterclockwise, , deltaphi= 15
       point= (  -WW/2   , -BB )
       point= (  -WW/2   , -(GuideGap/2+ RR2) )
          arc, radius= RR2, size= small, type= clockwise
       point= (  -(WW/2-RR2), -GuideGap/2 )

       # +x, -y
       point= (  (WW/2-RR2), -GuideGap/2 )
          arc, radius= RR2, size= small, type= clockwise
       point= (  WW/2   , -(GuideGap/2+ RR2) )
       point= (  WW/2   , -BB )
          arc, radius= RR5, size= small, type= counterclockwise, , deltaphi= 15
       point= (  GuideR0*cos(THETA), -GuideR0*sin(THETA) )
          arc, radius= GuideR0, size= small, type= counterclockwise, deltaphi= 5
       point= (  GuideR0, 0 ) # x', y'

   show= all
   doit

The figure 1.6 shows an outline of the waveguide that this decribes. This waveguide has its axis gowing in z-direction. Our waveguides shall have their axis lying in the x-y-plane, with an angle of 0, 120 and 240 degrees. In order to have the axis of our waveguide direct in the proper direction, we change the values of xprimedirection, yprimedirection. These two vectors define the local x', y' coordinate-system, in which the foorprint of the general cylinder is described. We edit our inputfile: 

 -ggcylinder
    material= 0
    range= ( 0, 100e-3 )

 define(PHI, 120*@pi/180 )
    xprimedirection= ( cos(PHI-@pi/2), sin(PHI-@pi/2), 0 )
    yprimedirection= ( 0, 0, 1 )
The resulting outline is shown in figure 1.7.
Figure 1.7: The waveguide now has its axis showing in the right direction.
\begin{figure}\centerline{ \psfig{figure=waveguide01.PS,width=14cm,bbllx=1pt,bblly=7pt,bburx=778pt,bbury=575pt,clip=} }\end{figure}

Modeling three straight waveguides

Since we have to model three waveguides, we could edit our inputfile to contain the description of the other waveguides as well. But this is a good opportunity to use a macro.

Anywhere in an inputfile we can define macros. A macro is enclosed between two lines: The first line contains the keyword macro followed by the name of the macro. All lines until a line with only the keyword endmacro are considered the body of the macro. When gd1 or gd1.pp find such a macro, they read it and store the body of the macro in an internal buffer.
Example 

   #
   # This defines a macro with name 'foo'
   #
   macro foo
      echo I am foo, my first argument is @arg1
      echo The total number of arguments supplied is @nargs
   endmacro
When gd1 or gd1.pp find a call of the macro, the number of the supplied arguments is assigned to the variable @nargs, and the variables @arg1, @arg2, .. are assigned the values of the supplied parameters of the call. The values of the arguments are strings. Of course it is possible to have a string eg. '1e-4' which happens to be interpreted in the right context as a real number.
Example 
   #
   # this calls 'foo' with the arguments 'hi', 'there'
   #
   call foo(hi, there)
Macro calls may be nested. The body of a macro may call another macro.

Macro 'Waveguide'

Since the three waveguides are at different angles, and their z-positions are to be changed, we parameterize our macro with arguments. We define a macro 'Waveguide' that expects two arguments: The first argument is the angle where the waveguide shall be placed, and the second argument is the z-position. 
 macro Waveguide
    define(Angle, @arg1)     # First argument of the macro
    define(ZPOSITION, @arg2) # Second argument
    
    define(GuideR0, 200e-3/2)
    define(GuideGap, 42.548e-3)
    define(WW, 51e-3)
    define(RR2, 2e-3)
    define(RR5, 5e-3)

 -ggcylinder
    material= 0
    range= ( 0, 100e-3 )

 define(PHI, Angle*@pi/180 )
    xprimedirection= ( cos(PHI-@pi/2), sin(PHI-@pi/2), 0 )
    yprimedirection= ( 0, 0, 1 )
    origin= ( 100*cos(PHI), 100*sin(PHI), ZPOSITION )

 define(AA, WW/2+RR5)
 define(BB, ((GuideR0-RR5)**2 - AA**2)**0.5)
 define(THETA, atan2(BB, AA))

    clear

       # +x, +y
       point= ( GuideR0, 0 ) # x', y'
          arc, radius= GuideR0, size= small, type= counterclockwise, deltaphi= 5
       point= ( GuideR0*cos(THETA), GuideR0*sin(THETA) )
          arc, radius= RR5, size= small, type= counterclockwise, , deltaphi= 15
       point= (  WW/2   , BB )
       point= (  WW/2   , GuideGap/2+ RR2 )
          arc, radius= RR2, size= small, type= clockwise
       point= (  WW/2-RR2 , GuideGap/2 )

       # -x, +y
       point= ( -(WW/2-RR2), GuideGap/2 )
          arc, radius= RR2, size= small, type= clockwise
       point= ( -WW/2   , GuideGap/2+ RR2 )
       point= ( -WW/2   , BB )
          arc, radius= RR5, size= small, type= counterclockwise, , deltaphi= 15
       point= ( -GuideR0*cos(THETA), GuideR0*sin(THETA) )
          arc, radius= GuideR0, size= small, type= counterclockwise, deltaphi= 5
       point= ( -GuideR0, 0 ) # x', y'

       # -x, -y
       point= ( -GuideR0, 0 ) # x', y'
          arc, radius= GuideR0, size= small, type= counterclockwise, deltaphi= 5
       point= ( -GuideR0*cos(THETA), -GuideR0*sin(THETA) )
          arc, radius= RR5, size= small, type= counterclockwise, , deltaphi= 15
       point= (  -WW/2   , -BB )
       point= (  -WW/2   , -(GuideGap/2+ RR2) )
          arc, radius= RR2, size= small, type= clockwise
       point= (  -(WW/2-RR2), -GuideGap/2 )

       # +x, -y
       point= (  (WW/2-RR2), -GuideGap/2 )
          arc, radius= RR2, size= small, type= clockwise
       point= (  WW/2   , -(GuideGap/2+ RR2) )
       point= (  WW/2   , -BB )
          arc, radius= RR5, size= small, type= counterclockwise, , deltaphi= 15
       point= (  GuideR0*cos(THETA), -GuideR0*sin(THETA) )
          arc, radius= GuideR0, size= small, type= counterclockwise, deltaphi= 5
       point= (  GuideR0, 0 ) # x', y'

   show= all
   doit
 endmacro

Modelling the real waveguides

The real waveguides consist of two parts. The cross-section of the first part is constant. The cross section of the second part varies continuously. As a further complication, the outer diameter of the second part varies as a linear function, while the gap of the waveguide varies nonlinear.

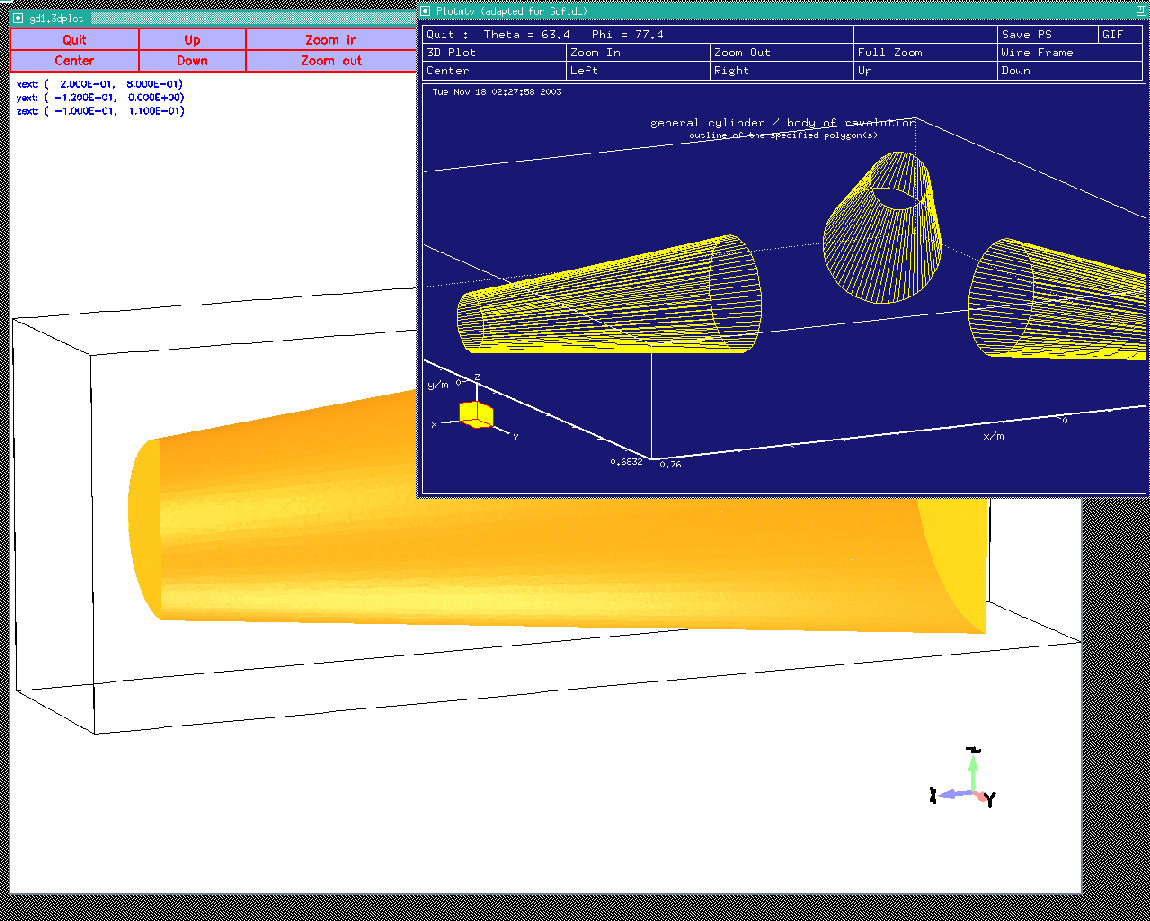
To be able to model the complicated second part, we model the waveguide in two steps. In the first step, we fill a volume with vacuum. This volume models the waveguide without the ridge, ie it is simply a circulare waveguide where the radius varies linearly. In a second step, the volume of the ridge is refilled with electric conducting material.

Figure 2.1: The radius of the waveguide and the gap of the ridge as a function of the position within the waveguide.
\begin{figure}\begin{center} \psfig{figure=scanned/function.PS,width=12cm} \end{center} \end{figure}

Macro 'Linear_Waveguide'

gd1 directly allows the modeling of cross-sections which vary as a linear function. 
 macro Linear_Waveguide
    define(zzPHI, @arg1 *@pi/180)     # First argument of the macro
    define(ZPOSITION, @arg2)          # Second argument
    
    define(GuideR0, @arg4)

 -ggcylinder
    material= 0
    range= ( @arg3, @arg5 )

    xprimedirection= ( cos(zzPHI+@pi/2), sin(zzPHI+@pi/2), 0 )
    yprimedirection= ( 0, 0, 1 )
    origin= ( 0, 0, ZPOSITION )

 xslope= (@arg6/@arg4-1)/(@arg5-@arg3)
 yslope= (@arg6/@arg4-1)/(@arg5-@arg3)

    clear

       point= ( GuideR0, 0 ) # x', y'
          arc, radius= GuideR0, size= small, type= counterclockwise, deltaphi= 5
       point= ( 0, GuideR0 )
          arc,
       point= ( -GuideR0, 0 )
          arc,
       point= ( 0, -GuideR0 )
          arc,
       point= ( GuideR0, 0 )

   show= @arg7 # now|later|all
   doit
 endmacro

 if (0) then
    #
    # for example, call the macro three times:
    #
    do Phi= 0, 240, 120
       if (Phi == 240) then
          sdefine(SHOW, all)
       else
          sdefine(SHOW, later)
       endif
    call Linear_Waveguide(Phi, \   # angle
                          10e-3, \ # z-position
                          260e-3, \           # starting position of the ggcylinder
                          100e-3, \           # start value outer radius
                          (260e-3+500e-3), \  # end position of the ggcylinder
                          50e-3, \            # endvalue of the outer radius
                          SHOW )
    enddo
 endif
Figure 2.2: Screenshot with the outline as produced by calling the macro 'Linear_Waveguide' three times with different parameters. In the background, an example of a generated mesh is shown.
\begin{figure}\begin{center}\psfig{figure=linear_waveguide.PS,width=723.0pt} \end{center} \end{figure}

Macro 'Linear_Ridge'

The gap of the ridge varies nonlinear. We model the nonlinear behaviour by modeling the ridge as many short sections where the gap may be assumed varying linear. 
 macro Linear_Ridge
    define(zzPHI, @arg1 *@pi/180)     # First argument of the macro
    define(ZPOSITION, @arg2)          # Second argument
    define(GuideGap, 2*(@arg4) )      # @arg4 : Half starting gap

    define(WW, 51e-3)
    define(RR2, 2e-3)
    define(RR5, 5e-3)
    
 -ggcylinder
    range= ( @arg3, @arg5 )

    xprimedirection= ( cos(zzPHI+@pi/2), sin(zzPHI+@pi/2), 0 )
    yprimedirection= ( 0, 0, 1 )
    origin= ( 0, 0, ZPOSITION )

    #
    # We first refill a larger part with
    # electric conducting material.
    #
    clear
       point= ( -WW/2, -100e-3 ) # x', y'
       point= (  WW/2, -100e-3 )
       point= (  WW/2,  100e-3 )
       point= ( -WW/2,  100e-3 )
    material= 3
    show= later
    xslope= 0, yslope= 0
    doit


    #
    # We now carve out the vacuum part
    #
    material= 0
 xslope= 0
 yslope= (@arg6/@arg4-1)/(@arg5-@arg3)

 define(AA, WW/2+RR5)
 define(BB, ((GuideR0-RR5)**2 - AA**2)**0.5)
 define(THETA, atan2(BB, AA))

    clear

       # +x, +y
       point= (  WW/2   , GuideGap/2+ RR2 )
          arc, radius= RR2, size= small, type= clockwise
       point= (  WW/2-RR2 , GuideGap/2 )

       # -x, +y
       point= ( -(WW/2-RR2), GuideGap/2 )
          arc, radius= RR2, size= small, type= clockwise
       point= ( -WW/2   , GuideGap/2+ RR2 )

       # -x, -y
       point= (  -WW/2   , -(GuideGap/2+ RR2) )
          arc, radius= RR2, size= small, type= clockwise
       point= (  -(WW/2-RR2), -GuideGap/2 )

       # +x, -y
       point= (  (WW/2-RR2), -GuideGap/2 )
          arc, radius= RR2, size= small, type= clockwise
       point= (  WW/2   , -(GuideGap/2+ RR2) )

   show= @arg7 # now|later|all
   doit
 endmacro

 #
 # Call the macro for example like this:
 #
 if (0) then
    call Linear_Ridge(0, \   # angle
                      10e-3, \ # z-position
                      260e-3, \           # starting position of the ggcylinder
                      43e-3, \           # start value half gap
                      (260e-3+500e-3), \  # end position of the ggcylinder
                      9e-3, \            # endvalue of half gap
                      all )
 endif
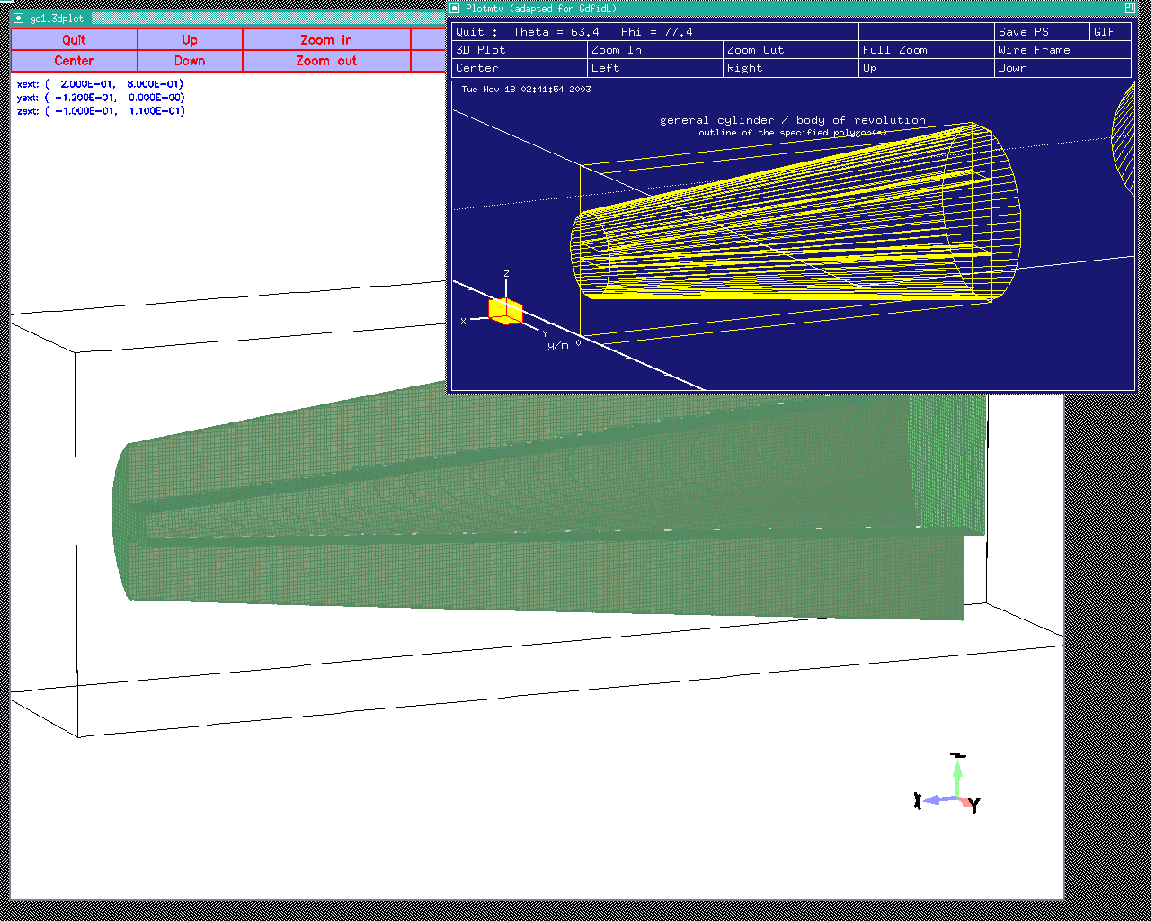
When we call the macro after the linear varying waveguide has been modeled, we get a plot similiar to the one shown in figure 2.3. The used inputfile is: 
 -brick
    material= 3
    volume= ( -INF,INF, -INF,INF, -INF,INF )
    doit

 include( macro-Linear_Waveguide.gdf )
 include( macro-Linear_Ridge.gdf )

 #
 # Call the macros three times:
 #
 do Phi= 0, 240, 120
    if (Phi == 240) then
       sdefine(SHOW, all)
    else
       sdefine(SHOW, later)
    endif
    call Linear_Waveguide(Phi, \   # angle
                          10e-3, \ # z-position
                          260e-3, \           # starting position of the ggcylinder
                          100e-3, \           # start value outer radius
                          (260e-3+500e-3), \  # end position of the ggcylinder
                          50e-3, \            # endvalue of the outer radius
                          later )


    call Linear_Ridge(Phi, \   # angle
                      10e-3, \ # z-position
                      260e-3, \           # starting position of the ggcylinder
                      43e-3, \           # start value half gap
                      (260e-3+500e-3), \  # end position of the ggcylinder
                      9e-3, \            # endvalue of half gap
                      SHOW )
 enddo


 -mesh
    perfectmesh= yes
    spacing= 2e-3
    pxlow= 0.2, pxhigh= 0.8
    pylow= -0.12, pyhigh= 0
    pzlow= -0.1, pzhigh= 0.11

 -volumeplot
     doit
Figure 2.3: Screenshot with the outline as produced by calling the macros 'Linear_waveguide' and 'Linear_Ridge' three times with different parameters. In the background, an example of a generated mesh is shown.
\begin{figure}\begin{center}\psfig{figure=linear_ridge.PS,width=723.0pt} \end{center} \end{figure}

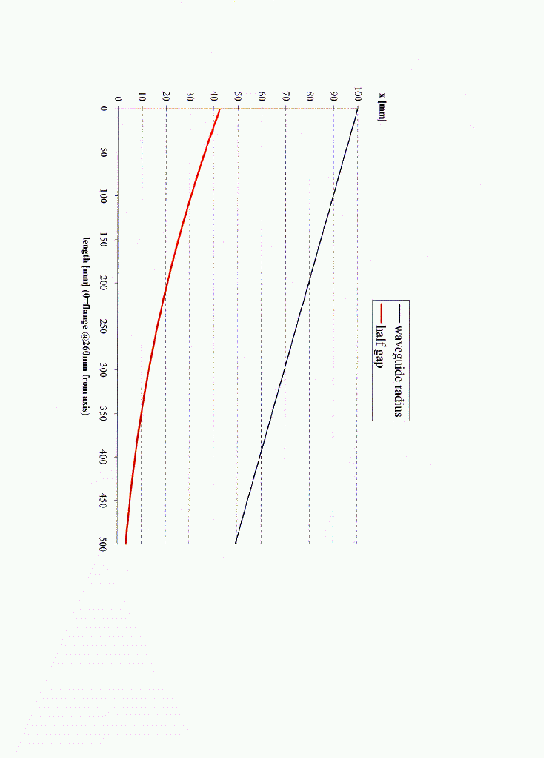
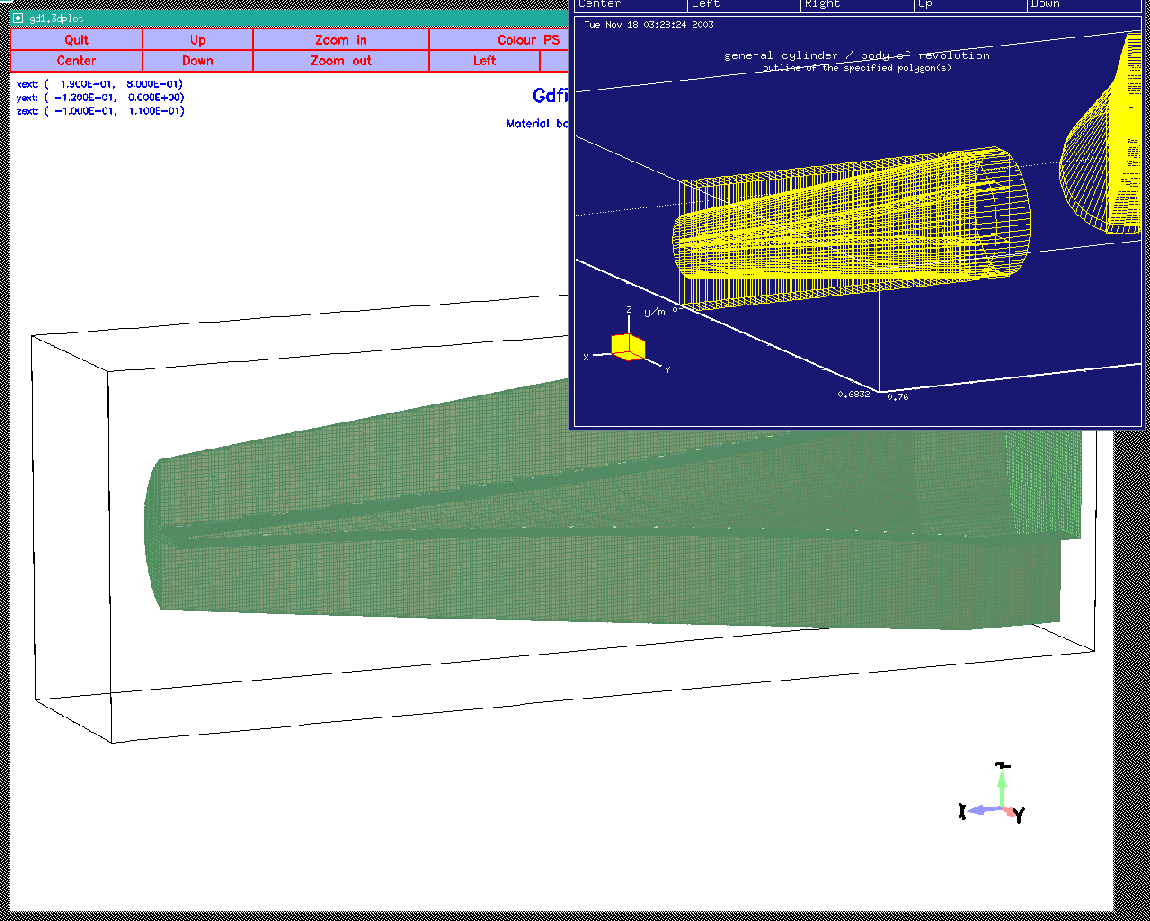
Since the real ridgevaries nonlinearly, we now have to call the macro many times with the proper start and end values. The wanted gap-widths as a function position can be taken from the dataset provided by Dr Marhauser: 

1. Waveguide Position
2. Waveguide Radius
3. Half Gap-distance
4. Distance measured from Cavity-adapter
5. Distance measured from Cavity-center
0       100             42.548  115     375
10      98.98448        41.2529 125     385
20      97.96896        39.9786 135     395
30      96.95344        38.7253 145     405
40      95.93792        37.4932 155     415
50      94.9224         36.2822 165     425
60      93.90688        35.0925 175     435
70      92.89136        33.9242 185     445
80      91.87584        32.7772 195     455
90      90.86032        31.6517 205     465
100     89.8448         30.5478 215     475
110     88.82928        29.4654 225     485
120     87.81376        28.4046 235     495
130     86.79824        27.3812 245     505
140     85.78272        26.3479 255     515
150     84.76720        25.3521 265     525
160     83.75168        24.378  275     535
170     82.73616        23.4255 285     545
180     81.72064        22.4947 295     555
190     80.70512        21.5856 305     565
200     79.68960        20.6981 315     575
210     78.67408        19.8322 325     585
220     77.65856        18.9879 335     595
230     76.64304        18.165  345     605
240     75.62752        17.3635 355     615
250     74.61200        16.5834 365     625
260     73.59648        15.8246 375     635
270     72.58096        15.0868 385     645
280     71.56544        14.3701 395     655
290     70.54992        13.6743 405     665
300     69.53440        12.9992 415     675
310     68.51888        12.3448 425     685
320     67.50336        11.7107 435     695
330     66.48784        11.0969 445     705
340     65.47232        10.5031 455     715
350     64.45680        9.92909 465     725
360     63.44128        9.3747  475     735
370     62.42576        8.83965 485     745
380     61.41024        8.32367 495     755
390     60.39472        7.82648 505     765
400     59.37920        7.3478  515     775
410     58.36368        6.88729 525     785
420     57.34816        6.44464 535     795
430     56.33264        6.01949 545     805
440     55.31712        5.61147 555     815
450     54.30160        5.22019 565     825
460     53.28608        4.84526 575     835
470     52.27056        4.48623 585     845
480     51.25504        4.14267 595     855
490     50.23952        3.8141  605     865
500     49.22400        3.5000  615     875
We can generate the needed calls to our function via a short program tha reads this dataset and then writes the appropriate file: 
 ! This is a small Fortran program which generates
 ! the appropriate calls.

    DO i= 1, 5
       READ (*,*) ! Skip the first five lines
    ENDDO

    DO
       READ (*,*) WPos, WRadius, HGap, DistAdapt, DistanceCenter
       WRITE (*,50) DistanceCenter*1e-3, HGap*1e-3
       WRITE (*,60) DistanceCenter*1e-3
       WRITE (*,70)                  HGap*1e-3
    ENDDO

 50 FORMAT(' call Linear_Ridge(Phi, ZPOS,', &
            G17.7,', ', G17.7,', POS_OLD, G_OLD, later )')
 60 FORMAT(' ')
 70 FORMAT(' ')

    END
The inputfile with the automaticalls generated calls: 
 -brick
    material= 3
    volume= ( -INF,INF, -INF,INF, -INF,INF )
    doit

 include( macro-Linear_Waveguide.gdf )
 include( macro-Linear_Ridge.gdf )

 #
 # Call the macros three times:
 #
 do Phi= 0, 240, 120
    if (Phi == 240) then
       sdefine(SHOW, all)
    else
       sdefine(SHOW, later)
    endif
 define(ZPOS, 10e-3)

    #
    # constant radius section:
    #
    call Linear_Waveguide(Phi, \   # angle
                          ZPOS, \ # z-position
                          200e-3, \           # starting position of the ggcylinder
                          100e-3, \           # start value outer radius
                          375e-3, \  # end position of the ggcylinder
                          100e-3, \            # endvalue of the outer radius
                          later )

    #
    # linear varying section:
    #
    call Linear_Waveguide(Phi, \   # angle
                          ZPOS, \ # z-position
                          375e-3, \           # starting position of the ggcylinder
                          100e-3, \           # start value outer radius
                          (375e-3+500e-3), \  # end position of the ggcylinder
                          50e-3, \            # endvalue of the outer radius
                          later )



 define(POS_OLD,    0.200000     ) # inserted by hand
 define(G_OLD,    0.4254800E-01 )  # inserted by hand
 #
 # The automatically generated part of the inputfile:
 #
 call Linear_Ridge(Phi, ZPOS,    0.2600000    ,     0.4254800E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.2600000     )
 define(G_OLD,    0.4254800E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.2700000    ,     0.4125290E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.2700000     )
 define(G_OLD,    0.4125290E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.2800000    ,     0.3997860E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.2800000     )
 define(G_OLD,    0.3997860E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.2900000    ,     0.3872530E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.2900000     )
 define(G_OLD,    0.3872530E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.3000000    ,     0.3749320E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.3000000     )
 define(G_OLD,    0.3749320E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.3100000    ,     0.3628220E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.3100000     )
 define(G_OLD,    0.3628220E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.3200000    ,     0.3509250E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.3200000     )
 define(G_OLD,    0.3509250E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.3300000    ,     0.3392420E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.3300000     )
 define(G_OLD,    0.3392420E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.3400000    ,     0.3277720E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.3400000     )
 define(G_OLD,    0.3277720E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.3500000    ,     0.3165170E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.3500000     )
 define(G_OLD,    0.3165170E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.3600000    ,     0.3054780E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.3600000     )
 define(G_OLD,    0.3054780E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.3700000    ,     0.2946540E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.3700000     )
 define(G_OLD,    0.2946540E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.3800000    ,     0.2840460E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.3800000     )
 define(G_OLD,    0.2840460E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.3900000    ,     0.2738120E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.3900000     )
 define(G_OLD,    0.2738120E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.4000000    ,     0.2634790E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.4000000     )
 define(G_OLD,    0.2634790E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.4100000    ,     0.2535210E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.4100000     )
 define(G_OLD,    0.2535210E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.4200000    ,     0.2437800E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.4200000     )
 define(G_OLD,    0.2437800E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.4300000    ,     0.2342550E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.4300000     )
 define(G_OLD,    0.2342550E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.4400000    ,     0.2249470E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.4400000     )
 define(G_OLD,    0.2249470E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.4500000    ,     0.2158560E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.4500000     )
 define(G_OLD,    0.2158560E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.4600000    ,     0.2069810E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.4600000     )
 define(G_OLD,    0.2069810E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.4700000    ,     0.1983220E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.4700000     )
 define(G_OLD,    0.1983220E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.4800000    ,     0.1898790E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.4800000     )
 define(G_OLD,    0.1898790E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.4900000    ,     0.1816500E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.4900000     )
 define(G_OLD,    0.1816500E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.5000000    ,     0.1736350E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.5000000     )
 define(G_OLD,    0.1736350E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.5100001    ,     0.1658340E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.5100001     )
 define(G_OLD,    0.1658340E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.5200000    ,     0.1582460E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.5200000     )
 define(G_OLD,    0.1582460E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.5300000    ,     0.1508680E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.5300000     )
 define(G_OLD,    0.1508680E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.5400000    ,     0.1437010E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.5400000     )
 define(G_OLD,    0.1437010E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.5500000    ,     0.1367430E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.5500000     )
 define(G_OLD,    0.1367430E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.5600000    ,     0.1299920E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.5600000     )
 define(G_OLD,    0.1299920E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.5700001    ,     0.1234480E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.5700001     )
 define(G_OLD,    0.1234480E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.5800000    ,     0.1171070E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.5800000     )
 define(G_OLD,    0.1171070E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.5900000    ,     0.1109690E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.5900000     )
 define(G_OLD,    0.1109690E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.6000000    ,     0.1050310E-01, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.6000000     )
 define(G_OLD,    0.1050310E-01 )
 call Linear_Ridge(Phi, ZPOS,    0.6100000    ,     0.9929090E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.6100000     )
 define(G_OLD,    0.9929090E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.6200000    ,     0.9374700E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.6200000     )
 define(G_OLD,    0.9374700E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.6300001    ,     0.8839651E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.6300001     )
 define(G_OLD,    0.8839651E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.6400000    ,     0.8323670E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.6400000     )
 define(G_OLD,    0.8323670E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.6500000    ,     0.7826480E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.6500000     )
 define(G_OLD,    0.7826480E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.6600000    ,     0.7347800E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.6600000     )
 define(G_OLD,    0.7347800E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.6700000    ,     0.6887290E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.6700000     )
 define(G_OLD,    0.6887290E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.6800000    ,     0.6444640E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.6800000     )
 define(G_OLD,    0.6444640E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.6900001    ,     0.6019490E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.6900001     )
 define(G_OLD,    0.6019490E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.7000000    ,     0.5611470E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.7000000     )
 define(G_OLD,    0.5611470E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.7100000    ,     0.5220190E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.7100000     )
 define(G_OLD,    0.5220190E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.7200000    ,     0.4845260E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.7200000     )
 define(G_OLD,    0.4845260E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.7300000    ,     0.4486230E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.7300000     )
 define(G_OLD,    0.4486230E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.7400000    ,     0.4142670E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.7400000     )
 define(G_OLD,    0.4142670E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.7500001    ,     0.3814100E-02, POS_OLD, G_OLD, later )
 define(POS_OLD,    0.7500001     )
 define(G_OLD,    0.3814100E-02 )
 call Linear_Ridge(Phi, ZPOS,    0.7600001    ,     0.3500000E-02, POS_OLD, G_OLD, SHOW )
 define(POS_OLD,    0.7600001     )
 define(G_OLD,    0.3500000E-02 )

 enddo


 -mesh
    perfectmesh= yes
    spacing= 2e-3
    pxlow= 0.19, pxhigh= 0.8
    pylow= -0.12, pyhigh= 0
    pzlow= -0.1, pzhigh= 0.11

 -volumeplot
     doit
Figure 2.4: Screenshot with the outline as produced by the many calls of the macros. In the background, an example of a generated mesh is shown.
\begin{figure}\begin{center}\psfig{figure=many-calls.PS,width=723.0pt} \end{center} \end{figure}

Modeling the transformer and the coaxial waveguides

The transformer can be modeled by filling cylinders with a general footprint near the end of the varying waveguide. 
 macro transformer
    define(zzPHI, (@arg1)*@pi/180 )
    define(ZOFF, @arg2)

    define(RALT, 50e-3) # The last radius
    -ggcyl
         material= 1
         xprime= ( cos(zzPHI      ), sin(zzPHI      ), 0 )
         yprime= ( cos(zzPHI+@pi/2), sin(zzPHI+@pi/2), 0 )
         xslope= 0, yslope= 0
 define(RR, 906.0e-3 - 31e-3)
 echo *** r-Position of tip of ellipse: eval(RR+31e-3) ( should be 906.0e-3 )
         origin= ( RR*cos(zzPHI), RR*sin(zzPHI), ZOFF )
         clear
            point= ( 0, -51e-3/2 )
               ellipse, center= ( 0, 0 ), size= small
            point= ( 31e-3, 0 )
               ellipse
            point= ( 0,  51e-3/2 )
         range= ( 3.5e-3, RALT )
    show= later
         doit
         range= ( -RALT, -3.5e-3 )
    show= @arg3
         doit

 endmacro

 if (0) then
    #
    # Call this macro eg like this:
    #
    call transformer(0, 0, later )
 endif
Figure 2.5: An outline of the general cylinder that shall decribe a transformer.
\begin{figure}\centerline{ \psfig{figure=transformer00.PS,width=14cm,bbllx=23pt,bblly=95pt,bburx=512pt,bbury=775pt,clip=} }\end{figure}

The coaxial waveguides are easily described as circular cylinders. In the first step, a circular cylinder is carved out with a radius of the outer conductor. In the second step, the volume of the inner conductor is refilled. We add these cylinders to the previous macro and get: 

 macro transformer_and_coaxial
    define(zzPHI, (@arg1)*@pi/180 )
    define(ZOFF, @arg2)

    define(RALT, 50e-3) # The last radius
    -ggcyl
         material= 3
         xprime= ( cos(zzPHI      ), sin(zzPHI      ), 0 )
         yprime= ( cos(zzPHI+@pi/2), sin(zzPHI+@pi/2), 0 )
         xslope= 0, yslope= 0
 define(RR, 906.0e-3 - 31e-3)
 echo *** r-Position of tip of ellipse: eval(RR+31e-3) ( should be 906.0e-3 )
         origin= ( RR*cos(zzPHI), RR*sin(zzPHI), ZOFF )
         clear
            point= ( 0, -51e-3/2 )
               ellipse, center= ( 0, 0 ), size= small
            point= ( 31e-3, 0 )
               ellipse
            point= ( 0,  51e-3/2 )
         range= ( 3.5e-3, RALT )
    show= later
         doit
         range= ( -RALT, -3.5e-3 )
    show= @arg3
         doit

    #
    # The coaxial line:
    #
    ### r-Position of coaxial lines:
    define(RR, 894.2e-3-19.2e-3)

    define(XOFF, (RR+19.2e-3)*cos(zzPHI) )
    define(YOFF, (RR+19.2e-3)*sin(zzPHI) )

    -mesh
       zfixed( 2, -3.5e-3+ZOFF, 3.5+ZOFF )
       xfixed( 3, XOFF-19.4e-3, XOFF- 8.4e-3 )
       yfixed( 3, YOFF-19.4e-3, YOFF- 8.4e-3 )
       xfixed( 3, XOFF+ 8.4e-3, XOFF+19.4e-3 )
       yfixed( 3, YOFF+ 8.4e-3, YOFF+19.4e-3 )

    -gccylinder
       length= INF
       origin= ( XOFF, YOFF, ZOFF-3.5e-3 )
       direction= ( 0, 0, 1 )
       material= 0, radius= 19.4e-3/2, doit   # Carve out radius of outer conductor

       origin= ( XOFF, YOFF, ZOFF-4.5e-3 )
       material= 4, radius=  8.4e-3/2, doit   # Refill inner conductor

 endmacro

 # call transformer_and_coaxial(Phi, Zpos, later)
Figure 2.6: Screenshot with the outline as produced by the many calls of the macros. In the background, an example of a generated mesh is shown. The used inputfile can be found as 'almost-done.gdf'.
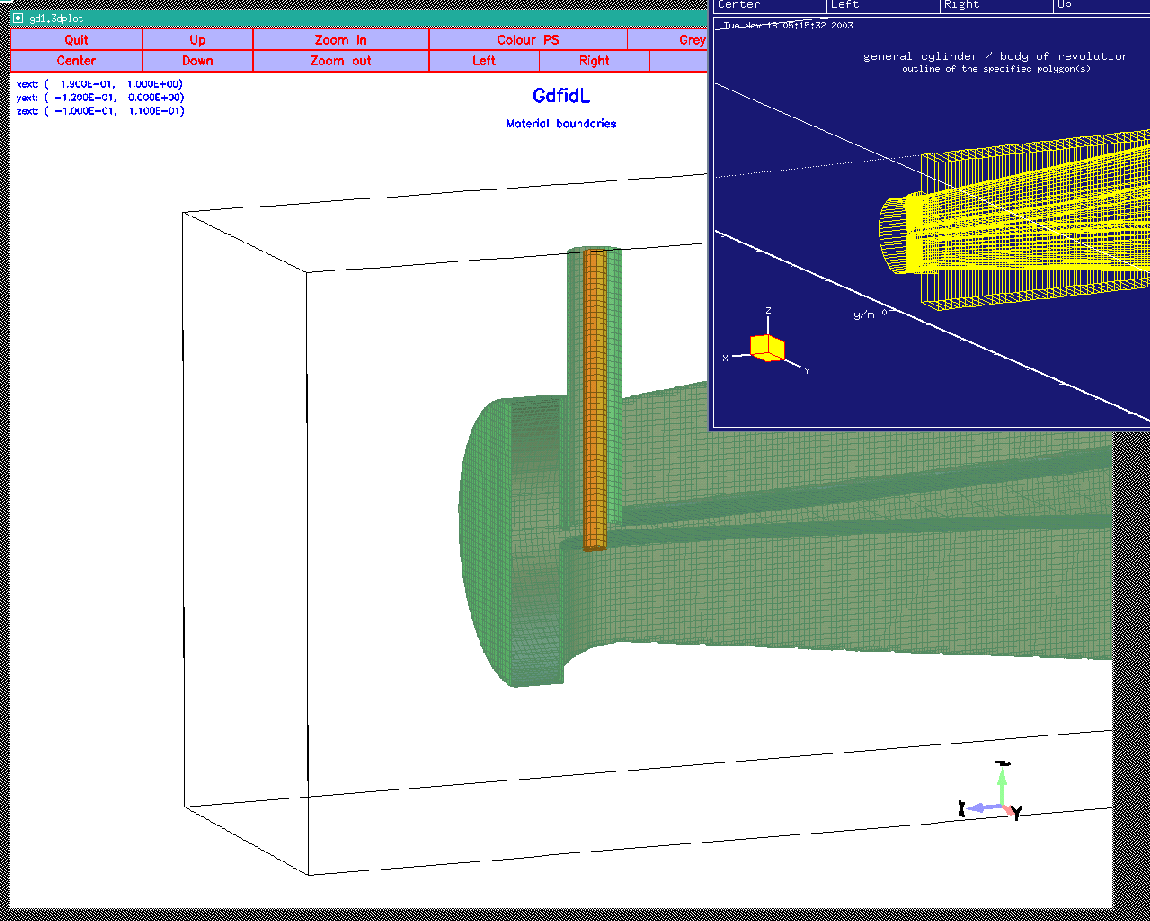\begin{figure}\begin{center}\psfig{figure=almost-done.PS,width=723.0pt} \end{center} \end{figure}

Putting it all together

We are now in the position to but it all together. The steps to model the geometry are: Fill the whole computational volume with vacuum, then carve out the waveguides, then carve out the cavity itself. As a last step, the ports need to be defined. If we do not use the symmetry plane at y=0 ($\varphi=0$), we have four ports ,the beam pipe and the three coaxial lines, at the upper z-boundary of the computational volume, and one port, the lower beam pipe, at the lower z-boundary. 
 -general
    outfile= /tmp/UserName/bessy-cavity
    scratch= /tmp/UserName/bessy-scratch-

    dice= yes   # If computing in parallel, use the subvolume algorithm
##    ndpw= 24    # use 24 subvolumes per CPU
    iodice= yes # store the results on the local discs of the nodes

 -material
    material= 3, type= electric
    material= 4, type= electric

 define(STPSZE, 2e-3)
 -mesh
    spacing= STPSZE

    #
    # The borders of the computational volume:
    #
 define(YLOW, -0.94)
 define(YHIGH, 0)
    pxlow= -0.6, pxhigh= 1.0
    pylow= YLOW, pyhigh= YHIGH
    pzlow= -0.2, pzhigh= 0.2

    #
    # The conditions at the borders:
    #
    cxlow= electric, cxhigh= electric
    cylow= electric, cyhigh= magnetic
    czlow= electric, czhigh= electric

 -brick
    material= 3
    volume= ( -INF,INF, -INF,INF, -INF,INF )
    doit

 include( macro-Linear_Waveguide.gdf )
 include( macro-Linear_Ridge.gdf )
 include( macro-transformer-and-coaxial.gdf )

 #
 # Call the macros three times:
 #
 do iPhi= 1, 3
    if (iPhi == 3) then
       sdefine(SHOW, all)
    else
       sdefine(SHOW, later)
    endif
    if (iPhi == 1) then
       define(ZPOS, 0.0495)
    else
       define(ZPOS, -0.0495)
    endif

 define(Phi, 0+(iPhi-1)*120)

    #
    # constant radius section of the circular part:
    #
    call Linear_Waveguide(Phi, \   # angle
                          ZPOS, \  # z-position
                          170e-3, \   # starting position of the ggcylinder
                          100e-3, \   # start value outer radius
                          375e-3, \   # end position of the ggcylinder
                          100e-3, \   # endvalue of the outer radius
                          later )

    #
    # constant section of the ridge:
    #
    call Linear_Ridge(Phi, \   # angle
                      ZPOS, \  # z-position
                      200e-3, \    # starting position of the ggcylinder
                      43e-3, \     # start value half gap
                      375e-3, \    # end position of the ggcylinder
                      9e-3, \      # endvalue of half gap
                      later )


    #
    # linear varying section:
    #
    call Linear_Waveguide(Phi, \   # angle
                          ZPOS, \ # z-position
                          375e-3, \  # starting position of the ggcylinder
                          100e-3, \  # start value outer radius
                          875e-3, \  # end position of the ggcylinder
                          50e-3, \   # endvalue of the outer radius
                          later )

    #
    # constant radius section, the part where the transformer is in
    #
    call Linear_Waveguide(Phi, \   # angle
                          ZPOS, \ # z-position
                          875e-3, \        # starting position of the ggcylinder
                          50e-3, \         # start value outer radius
                          (875e-3+65e-3), \  # end position of the ggcylinder
                          50e-3, \            # endvalue of the outer radius
                          later )


     #
     # Model the non-linear ridge via the many calls:
     #
     include( non-linear-ridge.gdf )

     #
     # Model the transformer and the coaxial line:
     #
     call transformer_and_coaxial(Phi, ZPOS, SHOW )

     #
     # tell GdfidL that the coaxial lines
     # shall be treated as ports.
     #
 define(XX, 900e-3*cos(Phi*@pi/180) )
 define(YY, 900e-3*sin(Phi*@pi/180) )
 if (YY+50e-3 >= YLOW) then
    if (YY-50e-3 <= YHIGH) then
        #
        # Only specify the port
        # if at least a part of it
        # is really within the computational volume
        #
        -fdtd
           -ports
               name= coax-phi=Phi, plane= zhigh, npml= 20, modes= 1
                  pxlow= XX-50e-3, pxhigh= XX+50e-3
                  pylow= YY-50e-3, pyhigh= YY+50e-3
               doit
    endif
 endif

 enddo # iPhi-loop

 #
 # tell GdfidL that the beam-pipes
 # shall be treated as ports.
 #
 -fdtd
    -ports
        name= beamlow, plane= zlow, npml= 40, modes= 0
           pxlow= -100e-3, pxhigh= 100e-3
           pylow= -100e-3, pyhigh= 100e-3
        doit

        name= beamhigh, plane= zhigh, npml= 40, modes= 0
           pxlow= -100e-3, pxhigh= 100e-3
           pylow= -100e-3, pyhigh= 100e-3
        doit

 #
 # Model the cavity itself:
 #
 include(Cavity.gdf)

 -volumeplot
     doit

 #
 # Specify that we want to perform a wakepotential-computation:
 #
 -fdtd
    -lcharge
       charge= 1e-12
       xposition= 0
       yposition= 0
       sigma= 5*STPSZE
       shigh= 400

 #
 # start the computation:
 #
 -fdtd
    doit
This is the end of this tutorial.


Footnotes

... data1
from Dr Marhauser from Berliner Elektronen Synchrotron, BESSY
next_inactive up previous