next up previous


Where goes the Energy lost by the Beam?

Figure 1: A Quarter of the Device
\begin{figure}\centerline{ \psfig{figure=Volumeplot.PS,width=16cm,bbllx=0pt,bblly=0pt,bburx=768pt,bbury=564pt,clip=} }\end{figure}

Dr Alexei Blednykh of BNL had send us the Description of a Device where he wants to know where the Energy lost by the Beam goes. The Inputfile for this Device is Inputfile The Energy-Loss is the longitudinal Lossfactor. A Wakepotential Computation gives a Energy Loss of $k_z = 383 \times 10^{-15}$ Joules. 

   gd1 < Inputfile | tee Logfile
   echo "-gen, inf @last, -wakes, shigh= 0.1, doit" | gd1.pp

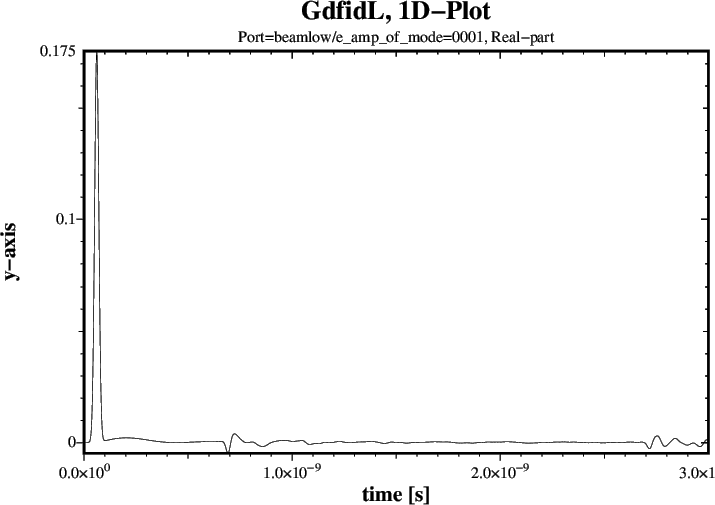
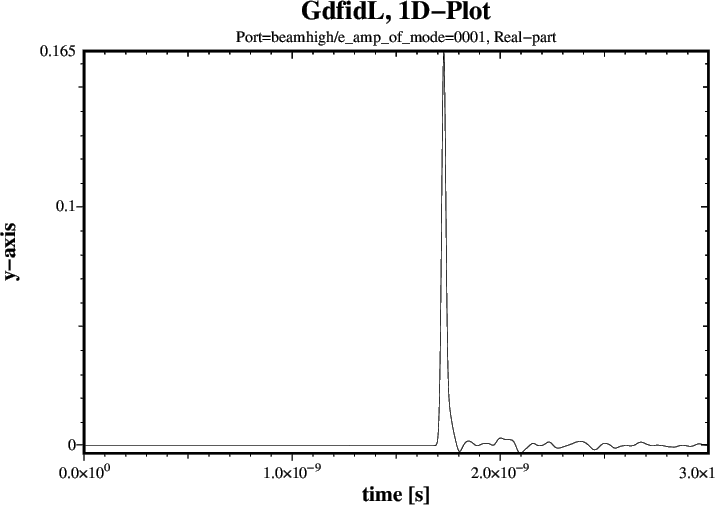
A Plot of the longitudinal Wakepotential is shown in Figure 2. The Lossfactor of $k_z = 383 \times 10^{-15}$ Newton-Meter is indicated in the upper right Corner. That Lossfactor as given by gd1.pp takes into Account the used two Planes of Symmetry.

Figure 2: The longitudinal Wakepotential up to s=0.1 Metres.
\begin{figure}\centerline{ \psfig{figure=wz.PS,width=16cm,bbllx=21pt,bblly=47pt,bburx=758pt,bbury=574pt,clip=} }\end{figure}

The Energy in the considered Volume will leave through the Ports. We have a Look at the Signals at the Ports: 

 # Input for gd1.pp:
   -general, inf @last
   -spara, freq no, time yes, upto 3e-9, doit
Three of the four resulting Plots are shown in Figures 3 through 5.
Figure 3: The Signal of the first Mode at Port1. The Signal is Zero up to t=0.35 $\times 10^{-9}$ Seconds. That is when the Beam passes the z-Position of the Port.
\begin{figure}\centerline{ \psfig{figure=Port1-Amp1.PS,width=16cm,bbllx=21pt,bblly=47pt,bburx=708pt,bbury=534pt,clip=} }\end{figure}
Figure 4: The Signal of the first Mode at BeamLow. The Signal should be Zero up to t= $ 2 \times 0.35 \times 10^{-9}$ Seconds, as that is the Time when the first scattered Fields, scattered at the z-Pos of Port1, can have reached the lower z-Plane where the Beam enters. The Signal is not zero in that Region, as the Beam-Field itself corrupts the Data.
\begin{figure}\centerline{ \psfig{figure=BeamLow-Amp1.PS,width=16cm,bbllx=21pt,bblly=47pt,bburx=708pt,bbury=534pt,clip=} }\end{figure}
Figure 5: The Signal of the first Mode at BeamHigh. The Signal is zero up to the Time when the Beam has traversed the whole computational Volume and has reached the upper z-Plane. The Signal near t=(zMax-zMin)/c = 1.7 nS is corrupted by the Beam-Field. Just while the Beam goes through the upper z-Plane, some scattered Field with high Group Velocity will also go through that upper z-Plane.
\begin{figure}\centerline{ \psfig{figure=BeamHigh-Amp1.PS,width=16cm,bbllx=21pt,bblly=47pt,bburx=708pt,bbury=534pt,clip=} }\end{figure}

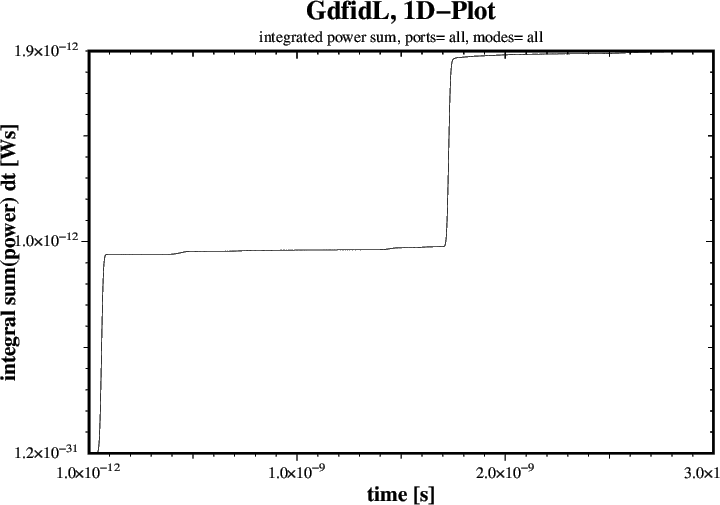
We compute the integrated Power Sum of all Modes: 

 # Input for gd1.pp:
   -general, inf @last
   -spara, freq no
      time no,  # time= yes, would give us Plots of all Signals.
      modes= all, ports= all
      tintpower= yes
      upto 3e-9
      doit
The resulting Plot is shown in Figure 6. The reported Power up to t=3nS is 1.9 $\times 10^{-12}$, much larger than the Lossfactor. The Result is so much larger, as the Signals are partly corrupted by the Beam-Fields.
Figure 6: The integrated Power in all Signals. The reported Power up to t=3nS is 1.9 $\times 10^{-12}$, much larger than the Lossfactor. The Result is so much larger, as the Signals are partly corrupted by the Beam-Fields.
\begin{figure}\centerline{ \psfig{figure=tintpower0.PS,width=16cm,bbllx=21pt,bblly=47pt,bburx=708pt,bbury=534pt,clip=} }\end{figure}
We compute the Power in the Signals which are corrupted by the Beam Fields by chopping off the Parts which are corrupted. 
 # Input for gd1.pp:
   -general, inf @last
   -spara, freq no 
      time no,  # time= yes, would give us Plots of all Signals.
      tintpower= yes
      upto 3e-9
      modes= all,
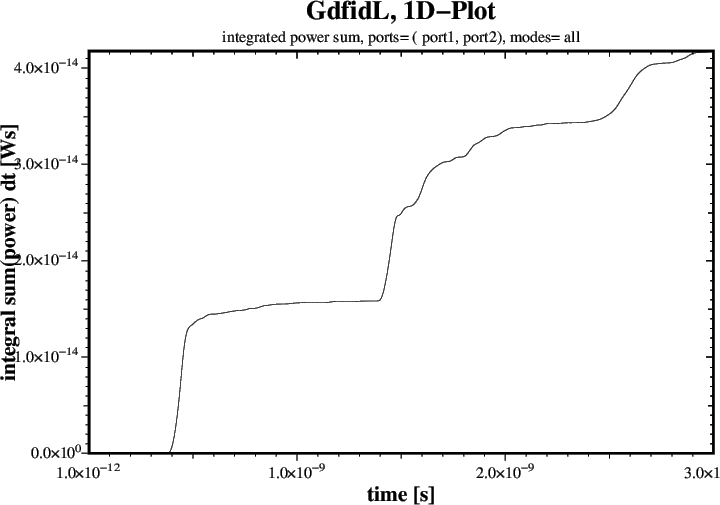
      ports= ( port1, port2), doit # These Signals are not corrupted.
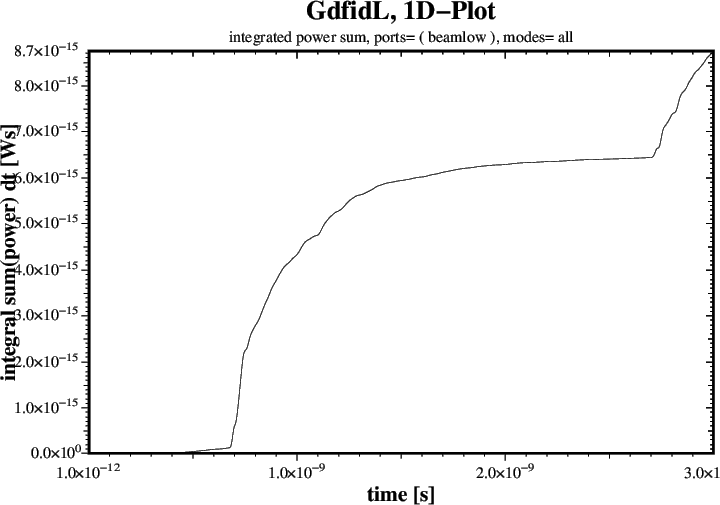
      tfirst= 0.4e-9, ports= ( beamlow ), doit # Corrupted up to t= 2*0.35e-9
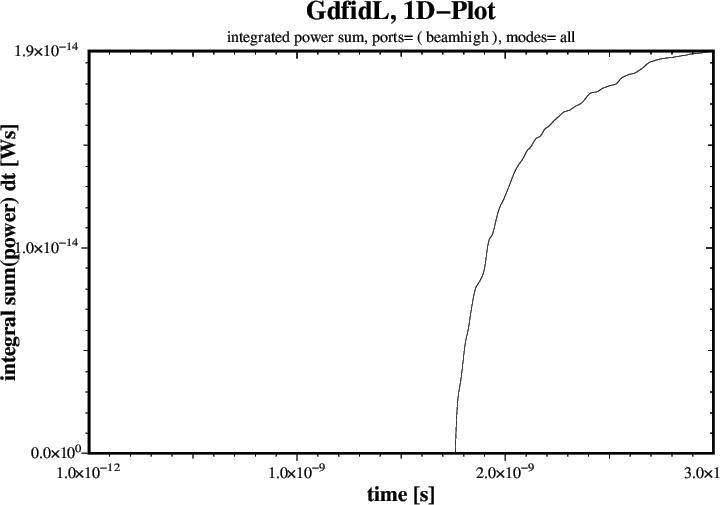
      tfirst= 1.76e-9, ports= ( beamhigh ), doit # Corrupted up to t= 1.76e-9
The resulting Plots are shown in Figures 7 through 9.
Figure 7: The integrated Power in all Signals at Port1 and Port2. Up to t= 3nS, $42 \times 10^-15$ Joules have left the Volume through these Ports.
\begin{figure}\centerline{ \psfig{figure=tintpowerPort1Port2.PS,width=16cm,bbllx=21pt,bblly=47pt,bburx=708pt,bbury=534pt,clip=} }\end{figure}
Figure 8: The integrated Power in all Signals at BeamLow. The Signals before t=0.4 nS are ignored. Up to t= 3nS, $8.7 \times 10^-15$ Joules have left the Volume through this Port.
\begin{figure}\centerline{ \psfig{figure=tintpowerBeamLow.PS,width=16cm,bbllx=21pt,bblly=47pt,bburx=708pt,bbury=534pt,clip=} }\end{figure}
Figure 9: The integrated Power in all Signals at BeamHigh. The Signals before t=1.76 nS are ignored. Up to t= 3nS, $19.5 \times 10^-15$ Joules have left the Volume through this Port.
\begin{figure}\centerline{ \psfig{figure=tintpowerBeamHigh.PS,width=16cm,bbllx=21pt,bblly=47pt,bburx=708pt,bbury=534pt,clip=} }\end{figure}
What is the Energy which at t=3 nS has not yet left the Volume? 
 # Input for gd1.pp:
   -general, inf @last
   -energy
       symbol= e_2, doit
       symbol= h_2, doit
This gives: 
 ##############################################################################
 # Flags: menu, prompt, message,                                              #
 ##############################################################################
 # Section: -energy                                                           #
 ##############################################################################
 # symbol   = h_2                                                             #
 # quantity = h                                                               #
 # solution = 2                                                               #
 # bbxlow =    -1.0000e+30, bbylow =    -1.0000e+30, bbzlow =    -1.0000e+30  #
 # bbxhigh=     1.0000e+30, bbyhigh=     1.0000e+30, bbzhigh=     1.0000e+30  #
 #                                                                            #
 #                                                                            #
 # @henergy : 6.45617e-15               (symbol: h_2, m: 1)                   #
 # @eenergy : 8.02293e-15               (symbol: e_2, m: 1)                   #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################
Our Energies so far: 
     6.45617e-15    # H-Energy at t=3e-9
     8.02293e-15    # E-Energy at t=3e-9
     42e-15         # Energy left through Port1 and Port2
     8.7e-15        # Energy left through BeamLow
     19.5e-15       # Energy left through BeamHigh
 Sum: 84.7e-15 Joules
$84.7 \times 10^{-15}$ Joules is much less than the Lossfactor of $383 \times 10^{-15}$ Joules. We have to multiply the $84.7 \times 10^{-15}$ Joules by Four, as we used the two Planes of Symmetry. This then gives $339 \times 10^{-15}$ Joules which have left the Volume or are still in the Volume. This is almost the Value of the Lossfactor. Where are the missing $(383-339) \times 10^{-15}$ Joules? They have left the Volume through the upper Port BeamHigh at Times when the Beam passed through the Port, and these Signals were chopped of.

next up previous