next_inactive up previous

How to compute the External Q of a loaded Cavity

The computation of the external Q of a cavity with an attached waveguide is via three simple steps.

First step, computation of resonant fields

In the first step, we compute the resonant fields in a closed geometry, ie. the waveguide is closed with an electric or magnetic boundary condition. 

    gd1 < cavity-with-waveguide.gdf | tee out-eigen

After some minutes we get a list of frequencies like: 

  One solution seems to be static and is not saved.
    i   freq(i)       acc(i)         cont(i)
    1   27.6778e+6   0.9982920236  0.3328254536       # "grep" for me
    2    2.8818e+9   0.0000000790  0.0000000695       # "grep" for me
    3    3.6905e+9   0.0000000162  0.0000000313       # "grep" for me
    4    4.5837e+9   0.0000000003  0.0000000005       # "grep" for me
    5    6.1361e+9   0.0000000103  0.0000000206       # "grep" for me
    6    6.4118e+9   0.0000000013  0.0000000151       # "grep" for me
    7    6.6111e+9   0.0000000084  0.0000000998       # "grep" for me
    8    6.8857e+9   0.0000000062  0.0000000463       # "grep" for me
    9    7.3426e+9   0.0000000095  0.0000000774       # "grep" for me
   10    7.5733e+9   0.0000005696  0.0000093463       # "grep" for me
   11    7.6269e+9   0.0000000112  0.0000001527       # "grep" for me
   12    7.9060e+9   0.0000000082  0.0000000684       # "grep" for me
   13    8.3725e+9   0.0013724901  0.0123083161       # "grep" for me
   14    8.4666e+9   0.0060409112  0.2701361389       # "grep" for me
The inputfile for this cavity is cavity-with-waveguide.gdf

Second step

We load the resonant field with the right frequency ( 2.88 GHz ) into the computational volume and let it ring. This time, we apply an absorbing boundary condition where the waveguide crosses the computational volume. We record the power flowing through that waveguide. 
     gd1 < let-it-ring.gdf | tee out-fdtd
The inputfile for this time-domain computation is let-it-ring.gdf

Third and last step

We use the postprocessor to look at the power flowing through the waveguide, and to compute the stored energy at a selected time. Since the cavity is only sligthly coupled, the power flowing is almost constant ( the external Q is very high ).

Figure 1: The power flowing through the waveguide as a function of time.
\begin{figure}\centerline{ \psfig{figure=tsumpower.PS,width=16cm,bbllx=21pt,bblly=47pt,bburx=708pt,bbury=534pt,clip=} }\end{figure}

We start the postprocessor, gd1.pp, and use him interactively:
Input for gd1.pp: 

     -general, infile= @last

     -sparameter
        freqdata= no
        timedata= yes
        tsumpower= yes
        doit
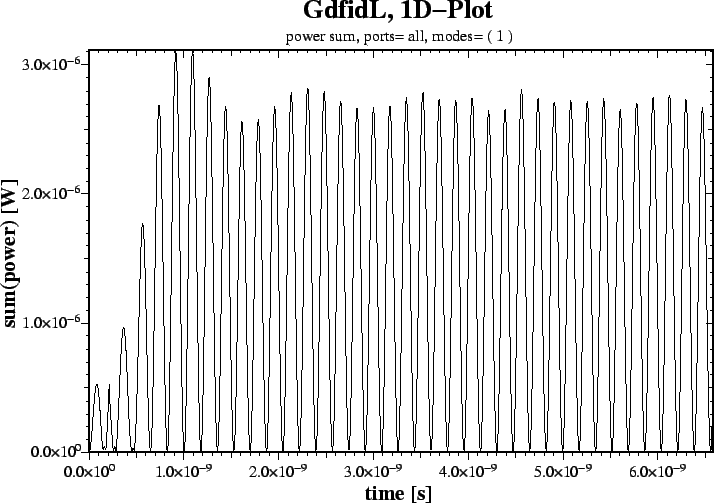
We get a lot of plots. One of these plots shows us the power sum of all selected modes as a function of time. ..But only one mode is selected.. After about 20 periods, the transients have decayed sufficiently, leaving only a $\sin^2(\omega t)$ function, which is the power as a function of time.
The average power is about 1.4e-6 Watts.
This is the radiated power.

In order to know the external Q, we have to know what the stored energy is. Since the power flowing is almost constant, the stored energy will also be almost constant...

We compute the stored energy in the electric and magnetic field with the section "-energy" of gd1.pp: 

    -energy
       solution= 8
       quantity= e, doit
       quantity= h, doit
     menu
We get the menu with 'menu' 
 ##############################################################################
 # Flags: nomenu, prompt, message,                                            #
 ##############################################################################
 # section: -energy                                                           #
 ##############################################################################
 # symbol   = h_8                                                             #
 # quantity = h                                                               #
 # solution = 8                                                               #
 #                                                                            #
 #                                                                            #
 # @henergy : 4.88692e-12               (symbol: h_8, m: 1)                   #
 # @eenergy : 253.6925e-15              (symbol: e_8, m: 1)                   #
 ##############################################################################
 # doit, ?, return, end, help                                                 #
 ##############################################################################
We see that at the time when the 8.th field was stored ( t=6.6901e-9 s ), the total stored energy in the computational volume was
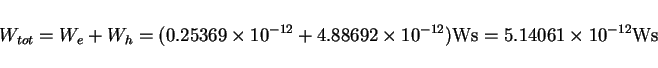\begin{displaymath} W_{tot} = W_e + W_h = ( 0.25369 \times 10^{-12} + 4.88692 \times 10^{-12} ) {\rm Ws} = 5.14061 \times 10^{-12} {\rm Ws} \end{displaymath} (1)

The external Q for the chosen aperture width therefore is

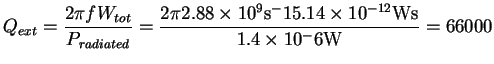$\displaystyle Q_{ext} = \frac{ 2 \pi f W_{tot} } { P_{radiated} } = \frac{ 2 \p... ...{\rm s}^-1 5.14 \times 10^{-12} {\rm Ws} } { 1.4 \times 10^-6 {\rm W} } = 66000$     (2)

 -------
 Thats it.
Although not necessary, we want to have a look at the electric field after about 20 periods:

Figure 2: The electric field after about 20 periods.
\begin{figure}\centerline{ \psfig{figure=e-feld.PS,width=18cm,bbllx=0pt,bblly=0pt,bburx=696pt,bbury=516pt,clip=} }\end{figure}


next_inactive up previous