 |
 |
GdfidL implements five different Schemes to compute Wakepotentials.
# The Yee-Scheme in a static Mesh. -fdtd, doit # Some higher Order Yee-Scheme in a static Mesh. -fdtd, hfdtd= yes, doit # The Yee-Scheme in a moving Mesh. -windowwake, strang= no, fdtdorder= 1, doit # Some other higher Order Yee-Scheme in a moving Mesh, -windowwake, strang= no, fdtdorder= 31, doit # Strang-Splitting in a moving Mesh. -windowwake, strang= yes, doit
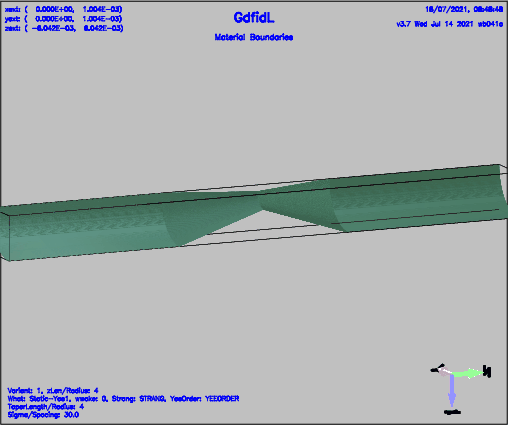
When the Grid-Spacing is small enough to make the Dispersion-Error negligable, and when the Absorbing-Boundary-Conditions work well, and when the Napoly-Intergration works well, all Schemes should give roughly the same Result, independent on the Length of straight Beampipes below and above the Wakefield scattering Obstacle. This Writeup demonstrates the Computation via the five Schemes, for different Lengths of straight Beampipes. The Device is a rotational-symmetric Collimator-Like Obstacle.
The Script to compute the Wakepotentials of the Device(s) loops over ThisVariant taking the Values 1,2,3,4,5
and over ThisZLen taking the Values 0, 4.
The outer Loop loops over ThisTLen taking the Values 4,8. With ThisTLen=4 it is a Device where the tapered Length is 4 x the Radius.
When ThisTLen=8, the tapered Length is 8 x the Radius.
When ThisTLen=16, the tapered Length is 16 x the Radius.
The Shell-Script tp compute all the Results is: check-Collimator.x
#!/bin/bash
for ThisTLen in 4 8 16
do
# When the Napoly-Integration is correct,
# and the Dispersion Error is negligable,
# and the Absorbing-Boundary-Conditions work good,
# the Result shall not depend on the Length of the straight Beampipes.
#
# ThisZLen: Length/Radius of the Beampipes
for ThisZLen in 0 4
do
# Compute the Results via five different Variants.
for ThisVariant in 1 2 3 4 5
do
gd1 -DVARIANT=$ThisVariant \
-DZLEN=$ThisZLen \
-DTLEN=$ThisTLen \
-DSCRATCH=/scratch/wb/ \
< CheckNapoly.gdf \
| tee Logfile-tLen-$ThisTLen-Variant-$ThisVariant-zLen-$ThisZLen
gd1.pp << UntilThisMarker
-gen, infile= @last
# This also defines the 'defines()' of the last Computation.
# In Particular, VARIANT, ZLEN and TLEN
-gen, scratch= /tmp/tLen-TLEN-Variant-VARIANT-zLen-ZLEN-
-wakes, onlyplotfiles= yes, doit
UntilThisMarker
done
# Start mymtv2 (plotmtv) showing the five Results in a single Plot.
mymtv2 -plotall -fg black -bg white \
/tmp/tLen-$ThisTLen-Variant-{1,2,3,4,5}-zLen-$ThisZLen-Wq_AT_XY.0001 &
mymtv2 -plotall -fg black -bg white \
/tmp/tLen-$ThisTLen-Variant-{1,2,3,4,5}-zLen-$ThisZLen-WYq_AT_XY.0001 &
done
done
exit 0
The Inputfile decribing the Device is: CheckNapoly.gdf
define(PLOT, 0)
if (VARIANT == 1) then
sdefine(WHAT, Static-Yee1)
define(WWAKE, 0)
sdefine(HFDTD, no)
else if (VARIANT == 2) then
sdefine(WHAT, Static-Yee33)
define(WWAKE, 0)
sdefine(HFDTD, yes)
else if (VARIANT == 3) then
sdefine(WHAT, ww-Strang)
define(WWAKE, 1)
sdefine(STRANG, yes) define(YEEORDER, 4711)
else if (VARIANT == 4) then
sdefine(WHAT, ww-Yee1)
define(WWAKE, 1)
sdefine(STRANG, no) define(YEEORDER, 1)
else if (VARIANT == 5) then
sdefine(WHAT, ww-Yee31)
define(WWAKE, 1)
sdefine(STRANG, no) define(YEEORDER, 31)
else
echo bad Variant: VARIANT
stop
end if
define(A, 1e-3 ) # Radius of the Beampipes
define(B, A/3) # Radius of the narrowest Part.
define(GAP, TLEN*A)
# define(GAP, 8*A) # Strang gives somewhat different Wy.
define(STPSZE, A/80/3)
define(SIGMA, 30*STPSZE)
define(DY, 0.1*A) # y-Position of the Linecharge.
-gen,
text()= Variant: VARIANT, zLen/Radius: ZLEN, tLen/Radius: TLEN
text()= What: WHAT, wwake: WWAKE, Strang: STRANG, YeeOrder: YEEORDER
text()= TaperLength/Radius: eval(GAP/A)
text()= Sigma/Spacing: eval(SIGMA/STPSZE)
define( GEOSCALE, 1 )
# To make the Frequency of an Impedance-Plot to k*A:
# define( GEOSCALE, @clight/A/2/@pi )
-mesh, geoscale= GEOSCALE
-general
outfile= SCRATCH/Collimator-tLen-TLEN-Variant-VARIANT-zLen-ZLEN
scratch= SCRATCH/scratch-
-mesh
spacing= STPSZE
pxlow= 0, pxhigh= A+STPSZE, cxlow= mag, cxhigh= ele
pylow= 0, pyhigh= A+STPSZE, cylow= ele, cyhigh= ele
pzlow = - (GAP/2 + ZLEN*A + 10*STPSZE)
pzhigh= + (GAP/2 + ZLEN*A + 10*STPSZE)
-material, material= 3, type= electric, kappa= 56e6
# Fill the Universe with Metal.
-brick, material= 3, volume= ( -INF,INF, -INF,INF, -INF,INF ), doit
-gccylinder
material= 0, radius= A, length= INF
origin= ( 0, 0, GAP/2 )
direction= ( 0, 0, 1 )
doit # Upper Beampipe
material= 0, radius= A, length= INF
origin= ( 0, 0, -GAP/2 )
direction= ( 0, 0, -1 )
doit # Lower BeamPipe
# The Tapers.
-gbor,
material= 0, origin= ( 0, 0, 0 ), zprime= ( 0, 0, 1 ), rprime= ( 1, 0, 0 )
clear
point= (-GAP/2-STPSZE, 0) # ( Zi, Ri )
point= (-GAP/2-STPSZE, A)
point= (-GAP/2, A)
point= ( 0, B )
point= ( GAP/2, A)
point= ( GAP/2+STPSZE, A)
point= ( GAP/2+STPSZE, 0)
# show= now
doit
if (PLOT) then
-volumeplot, roty= 90, doit
end if
-fdtd
-ports
define(NPML, 40)
name= beamlow, plane= zlow, modes= 0, npml= NPML, doit
name= beamhigh, plane= zhigh, modes= 0, npml= NPML, doit
-lcharge
if (PLOT) then
showdata= yes
else
showdata= no
end if
charge= 1e-12, sigma= SIGMA
xposition= 0, yposition= DY
shigh= 12*SIGMA
if (0) then
# If one would want to create a Movie.
define(NDT, 0.5 * STPSZE * GEOSCALE / @clight) # Every Timestep
-fdtd, -fexport
system( rm SCRATCH/H-fields-iVar-VARIANT-* )
outfile= SCRATCH/H-fields-VARIANT-
what= h-fields
firstsaved= 1e-20
lastsaved= INF
distancesaved= NDT
bbxlow= -STPSZE/10, bbxhigh= STPSZE/10
bbylow= -INF, bbyhigh= INF
bbzlow= -INF, bbzhigh= INF
doit
end if
if (WWAKE) then
-windowwake, fdtdorder= YEEORDER, strang= STRANG, doit
else
-fdtd, hfdtd= HFDTD, doit
end if
A Quarter of the rotational symmetric Device is modeled. An electric Boundary Condition at the Plane of Symmetry at y=0 is applied. With that Conditions, the y-transverse Wakepotential is computed. The shown longitudinal Wakepotentials are not the Wakepotentials as would be seen by a Beam at x=y=0.
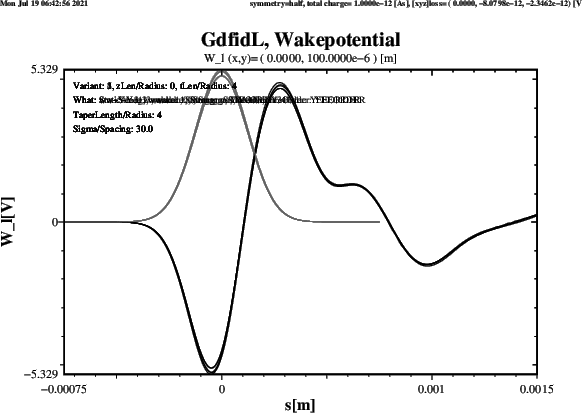
Plots of the computed longitudinal Wakepotential when ThisZLen has the Value 0,
ie. the upstream and downstream Beampipes are very short, are shown in Figure 3.
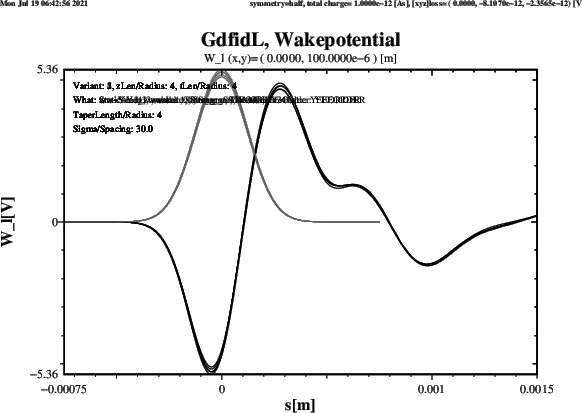
Plots of the computed longitudinal Wakepotential when ThisZLen has the Value 4,
ie. the upstream and downstream Beampipes are 4 times the Radius long, are shown in Figure 4.
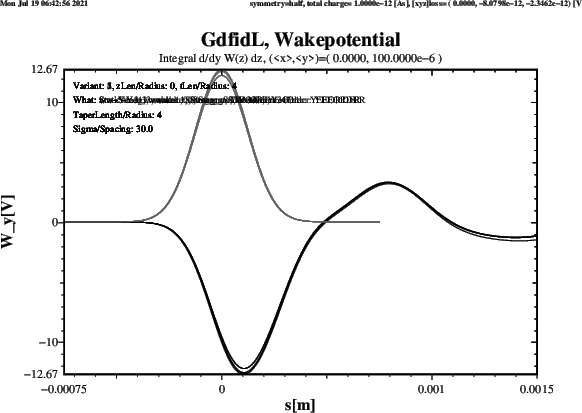
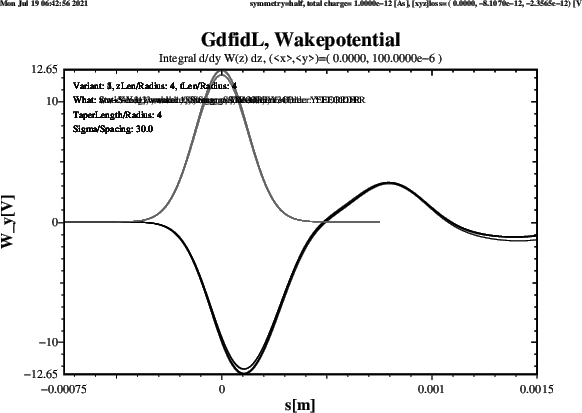
Plots of the computed transverse Wakepotential when ThisZLen has the Value 0,
ie. the upstream and downstream Beampipes are very short, are shown in Figure 5.
Plots of the computed transverse Wakepotential when ThisZLen has the Value 4,
ie. the upstream and downstream Beampipes are 4 times the Radius long, are shown in Figure 6.
The Results agree well. All five Schemes give about the same Result. The Length of the Beampipes does not change the Results significantly.
 |
 |
 |
 |
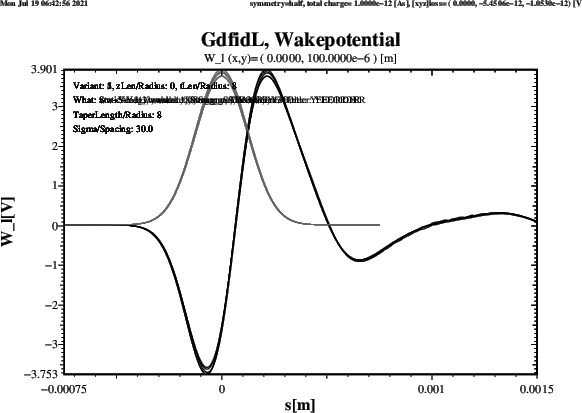
Plots of the computed longitudinal Wakepotential when ThisZLen has the Value 0,
ie. the upstream and downstream Beampipes are very short, are shown in Figure 7.
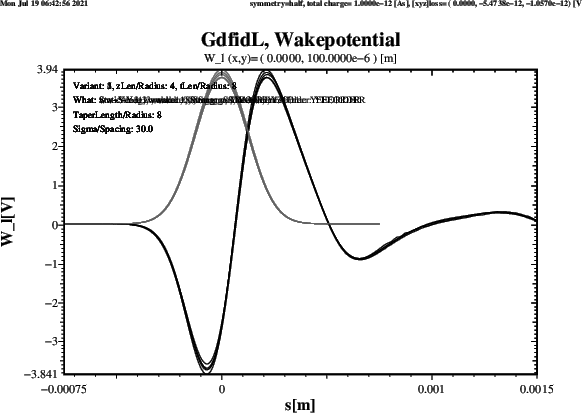
Plots of the computed longitudinal Wakepotential when ThisZLen has the Value 4,
ie. the upstream and downstream Beampipes are 4 times the Radius long, are shown in Figure 8.
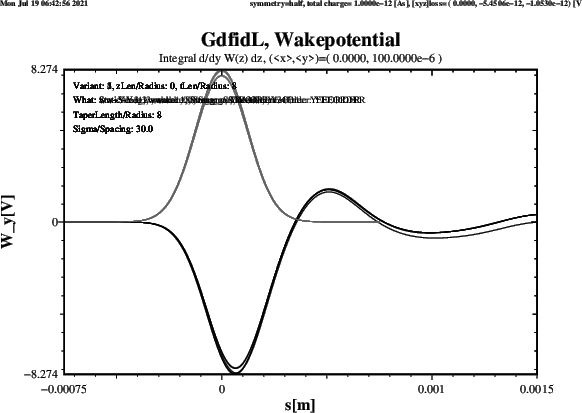
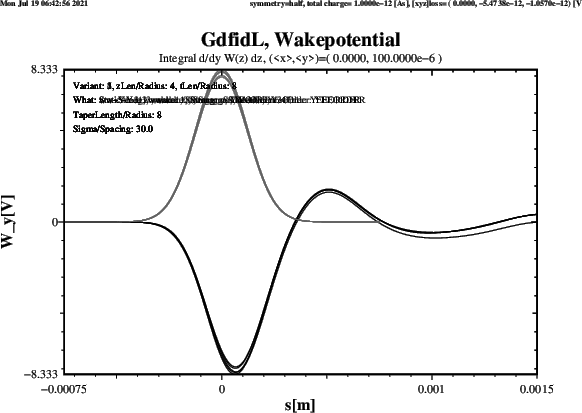
Plots of the computed transverse Wakepotential when ThisZLen has the Value 0,
ie. the upstream and downstream Beampipes are very short, are shown in Figure 9.
Plots of the computed transverse Wakepotential when ThisZLen has the Value 4,
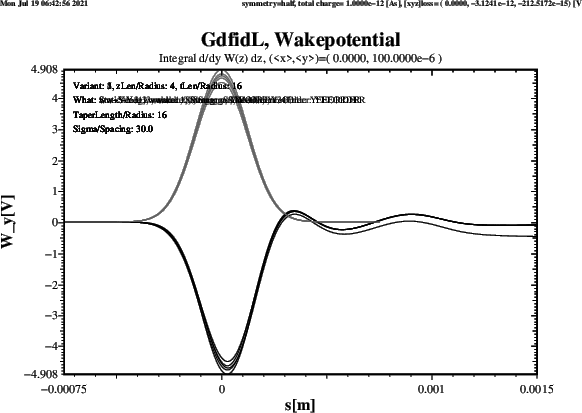
ie. the upstream and downstream Beampipes are 4 times the Radius long, are shown in Figure 10.
The Results agree well. Four Schemes give about the same Result. The Scheme which gives a significantly different Result for the Wy-Wakepotential is the Strang-Splitting Scheme. The Length of the Beampipes does not change the Results significantly.
 |
 |
 |
 |
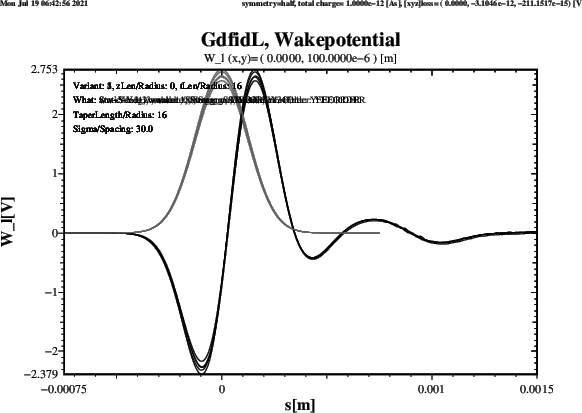
Plots of the computed longitudinal Wakepotential when ThisZLen has the Value 0,
ie. the upstream and downstream Beampipes are very short, are shown in Figure 11.
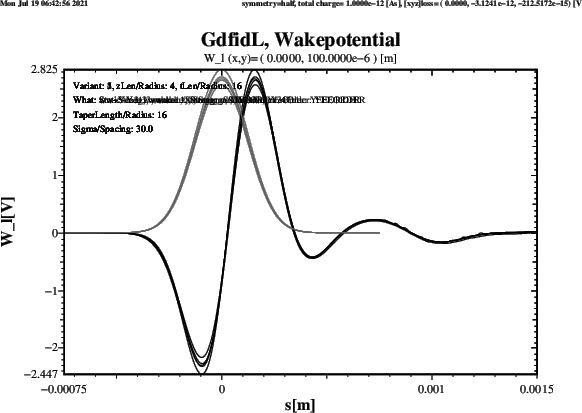
Plots of the computed longitudinal Wakepotential when ThisZLen has the Value 4,
ie. the upstream and downstream Beampipes are 4 times the Radius long, are shown in Figure 12.
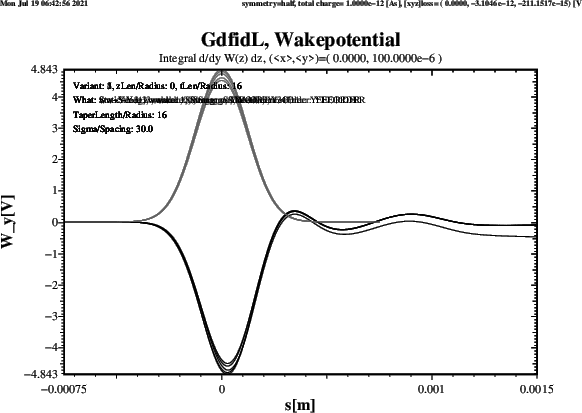
Plots of the computed transverse Wakepotential when ThisZLen has the Value 0,
ie. the upstream and downstream Beampipes are very short, are shown in Figure 13.
Plots of the computed transverse Wakepotential when ThisZLen has the Value 4,
ie. the upstream and downstream Beampipes are 4 times the Radius long, are shown in Figure 14.
The Results agree well. Four Schemes give about the same Result. The Scheme which gives a significantly different Result for the Wy-Wakepotential is the Strang-Splitting Scheme. The Length of the Beampipes does not change the Results significantly.
 |
 |
 |
 |
This is the End of this Writeup.